Анализ шума в частотной области

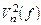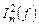Ввиду случайности и непредсказуемости значений шумового сигнала, его мощность (или ) непрерывно распределена в частотной области. Ввиду непрерывногораспределения, в бесконечно малой полосе частот мощность шума равна нулю! Когда говорят о конкретной спектральной плотности шума на какой-то частоте, то по умолчанию имеют в виду мощность шума в частотной полосе 1 Гц, и упомянутая частота находится в середине этой полосы. Полная мощность шума получается интегрированием плотности шума по всему спектру частот:

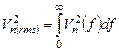(5.10)

Рассмотрим прохождение шумового сигнала 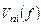через фильтр с передаточной функцией 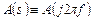. Спектральная плотность 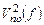мощности шума на выходе фильтра равна:

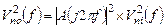(5.11)

Полная мощность шум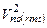а равна

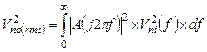(5.12)

Среднеквадратичное значение плотности шума 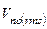равно

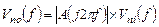(5.13)

Поскольку среднеквадратичное значение шума определяется обычным для линейного фильтра образом, посредством модуля передаточной функции, а не через ее квадрат, удобно пользоваться среднеквадратичным значением, а не мощностью шума.

Предположим теперь, что шум на выходе системы 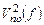является суммой 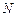входных шумовых сигналов 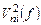, и каждый входной шумовой сигнал 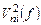проходит через фильтр 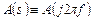. Тогда спектральная плотность 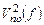шума на выходе:

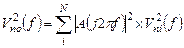(5.14)

Если шумовые сигналы взаимно не коррелированы, то на выходе фильтров они также не коррелированы.

5.1.3. Белый шум

«Белый шум»определяется как шум с постоянной и не зависящей от частоты спектральной плотностью шума. Наиболее известный источник белого шума – резистор. Шум резистора моделируется как включенный последовательно с резистором источник напряжения со спектральной плотностью :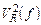

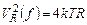(5.15а)

Здесь .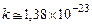

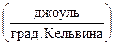Рис. 5.2. Эквивалентная схема шумящего резистора:

(a) – присоединенный последовательно источник шумового напряжения;

(b) – присоединенный параллельно источник шумового тока.

Следует отметить, что на общепринятом изображении шумящего резистора Ri с присоединенным последовательно источником шумового напряжения 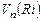символ самого источника шума ни в коей мере нельзя рассматривать как самостоятельный источник напряжения. В этой связи, например, на Рис. 5.2.а отсутствует узел между символами источника напряжения и резистора,поскольку их необходимо рассматривать как одно целое. Это необходимо учитывать при анализе и составлении уравнений Кирхгофа.

Наряду с моделью (5.15) в равной степени используется модель шума резистора как включенный параллельно с резистором источник тока со спектральной плотностью :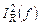

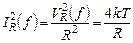. (5.15b)

5.1.4. Полоса шума

Как известно, идеальным фильтром является фильтр с прямоугольной АЧХ, в пределах которой модуль коэффициента передачи (усиление) равен единице, а в полосе задерживания равен нулю. Реальные фильтры имеют неравномерность АЧХ в полосе пропускания, конечный наклон в переходной полосе и отличное от нуля пропускание в полосе задерживания.

Рис.5.3. Реальный и идеальный

фильтры с идентичными

мощностями выходного шума

при одинаковых спектральных

плотностях белого шума

на входах.

Под полосой шума понимают полосу пропускания идеального прямоугольного фильтра низкой частоты, шум на выходе которого такой же, как на выходе рассматриваемого реального фильтра, при условии подключения на входы обоих фильтров одинаковых источников белого шума.

Представительным примером фильтра является пассивный RC фильтр первого порядка. Модулем его передаточной функции (зависимость коэффициента передачи от частоты) является выражение

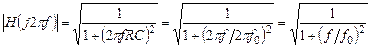(5.16)

где 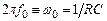– частота действительного полюса пассивного RС фильтра.

Подсоединим ко входу фильтра источник белого шума с независящей от частоты спектральной плотностью:

(5.17)

Полная мощность 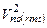шума, прошедшего через фильтр, равна:

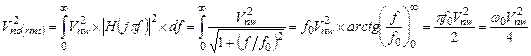(5.18)

Такой же по величине, но прошедший через идеальный прямоугольный фильтр низкой частоты с полосой 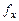, шум равен:

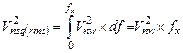(5.19)

Из сравнения (5.18) и (5.19) получаем:

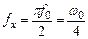(5.20)

Рассчитаем выражение для полной мощности шума напряжения на конденсаторе пассивного RC фильтра с шумящим резистором:

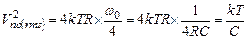(5.21)

Назначение приведенных выше выкладок – в том числе для получения фундаментального выражения (5.21), используемого при анализе аналоговых схем на переключаемых конденсаторах.