Покоординатный спуск
Покоординатный спуск обеспечивает наиболее простой по реализации алгоритм. В качестве возможных направлений рассматриваются орты исходной системы координат:
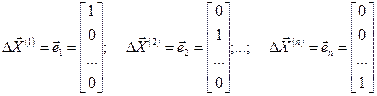
На первом итерационном шаге целевая функция 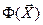 минимизируется при изменении только первой переменной, а все остальные переменные остаются неизменными (внутренний цикл):
минимизируется при изменении только первой переменной, а все остальные переменные остаются неизменными (внутренний цикл):
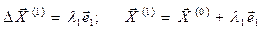
На втором шаге процедура повторяется для второй переменной:
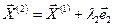 .
.
Минимизация по всем n переменным образует цикл, называемый внешним. Для большей определенности операции, связанные с изменениями переменных, внутри цикла называют шагами, а внешние циклы – итерациями.
Количество внешних циклов заранее неизвестно. Сходимостью вычислительного процесса зависит от свойств минимизируемой функции 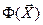 и выбора исходного приближения
и выбора исходного приближения 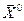 . Расходящегося процесса здесь быть не может, поскольку на каждом шаге имеет место уменьшение целевой функции. Однако, не может быть и полной гарантии получения решения, поскольку критерии сходимости основаны на произвольной априорной точности.
. Расходящегося процесса здесь быть не может, поскольку на каждом шаге имеет место уменьшение целевой функции. Однако, не может быть и полной гарантии получения решения, поскольку критерии сходимости основаны на произвольной априорной точности.
Градиентный метод
Движение осуществляется в направлении антиградиента - наибольшего убывания целевой функции:
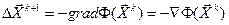
где 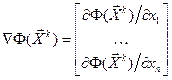 .
.
Дата добавления: 2020-07-18; просмотров: 530;











