Линейные преобразования
В линейном пространстве можно ввести функцию, ставящую в соответствие любому вектору 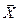 некоторый вектор
некоторый вектор  того же пространства:
того же пространства:
 ,
,
где 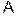 – функция преобразования пространства. Обозначение
– функция преобразования пространства. Обозначение 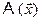 - называется оператором. Если вектор
- называется оператором. Если вектор 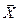 принадлежит одному пространству,
принадлежит одному пространству, 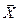 ÎV, а вектор
ÎV, а вектор  другому,
другому, 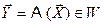 , то говорят о преобразовании пространств V®W. Если пространство преобразуется в себя V®V, то это линейное преобразование.
, то говорят о преобразовании пространств V®W. Если пространство преобразуется в себя V®V, то это линейное преобразование.
Вектор  - это образ вектора
- это образ вектора 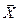 под действием преобразования
под действием преобразования 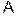 , а вектор
, а вектор 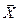 - прообраз вектора
- прообраз вектора  .
.
Преобразование называется линейным, если
1) 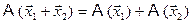 ;
;
2) 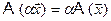 .
.
Пусть 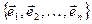 – некоторый базис в n- мерном пространстве Rn и
– некоторый базис в n- мерном пространстве Rn и 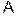 – линейное преобразование, тогда для его определения достаточно задать образы всех векторов базиса, т.е. величины:
– линейное преобразование, тогда для его определения достаточно задать образы всех векторов базиса, т.е. величины: 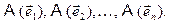 Покажем, что это так.
Покажем, что это так.
Если 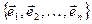 – базис, то для любого вектора
– базис, то для любого вектора 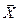 существует разложение:
существует разложение: 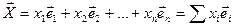
Используя свойства линейного преобразования, получаем:
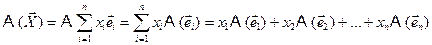
Если образы векторов базиса известны, то можно записать:
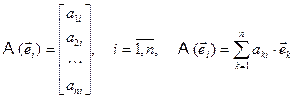 ,
,
поскольку 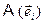 , как любой произвольный вектор, имеет разложение в существующем базисе. Тогда
, как любой произвольный вектор, имеет разложение в существующем базисе. Тогда
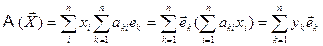 .
.
Отсюда 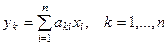 .
.
В результате 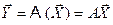 , где матрица А линейного преобразования есть матрица, столбцами которой являются образы базисных векторов. Таким образом, любые линейные преобразования можно описывать с помощью матриц и каждая матрица представляет некоторое линейное преобразование.
, где матрица А линейного преобразования есть матрица, столбцами которой являются образы базисных векторов. Таким образом, любые линейные преобразования можно описывать с помощью матриц и каждая матрица представляет некоторое линейное преобразование.
Пример. Линейное преобразование задано матрицей 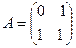 . Определить образ вектора
. Определить образ вектора  .
.
Решение 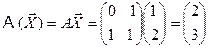 .
.
Определить прообраз вектора 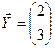 .
.
Решение. 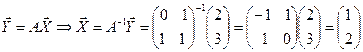 .
.
Дата добавления: 2020-07-18; просмотров: 634;











