Движущая сила диффузионного переноса.

Ранее уже говорилось, что причиной диффузии может быть любое неравновесное состояние, будь то градиент концентрации, упругих полей или других потенциалов. Рассмотрим причины диффузии с позиций термодинамики.

В соответствии с её законами частица 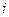-того сорта в растворе переходит из точки 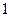в точку 2, если её химический потенциал в точке 1 больше, т.е. .

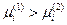Химический потенциал частицы 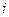- го сорта ( 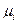) есть парциальный изобарно-изотермический потенциал определяемый как частная производная от изобарно-изотермического потенциала ( 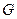) по числу частиц 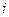-го компонента ( 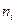) при условии, что давление ( 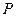), температура 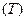и число частиц всех остальных компонентов 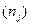остаются постоянными:

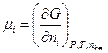(4.1)

Для перехода атомов 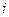-го сорта из точки 1 в точку 2 затрачивается работа, равная по величине и обратная по знаку изменению свободной энергии:

.

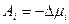Поскольку работа равна произведению силы 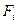на путь, то сила, действующая на атом

.

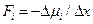В пределе, при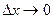

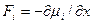
или для трехмерного случая:

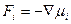(4.2)

Таким образом, движущая сила, вызывающая диффузионный перенос вещества 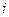-го сорта в многокомпонентной системе, определяется градиентом химического потенциала 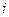-го компонента.

Под действием силы 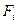атомы приходят в направленное движение со средней скоростью 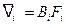, где 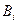- подвижность 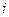-го компонента, т.е. скорость, которую приобретает частица под действием единичной силы. В результате возникает диффузионный поток

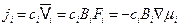. (4.3)

Для бесконечного разбавленного раствора химический потенциал 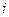-того компонента и его концентрацией зависимы как:

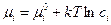, (4.4)

где 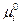- стандартный химический потенциал 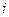-го компонента, 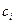- его концентрация, 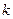- постоянная Больцмана, 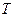- температура.

Подставляя уравнение (4.4) в (4.3), получим:

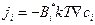. (4.5)

Звездочка обозначает бесконечно разбавленный раствор.

Сравнение (4.5) с первым уравнением Фика позволяет установить связь между коэффициентом диффузии и подвижностью

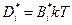. (4.6)

Это уравнение справедливо только для бесконечно разбавленного раствора ( 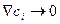), когда атом 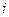-го сорта движется в практически постоянном силовом поле. Поэтому в левой его части стоит коэффициент изотопной диффузии ( ).

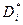В случае реального раствора, когда диффундирующий атом окружен меняющемся числом соседей разного сорта и движется в меняющемся силовом поле необходимо ввести в выражение (4.4) вместо концентрации активность ( 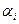) 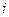-того компонента. Тогда

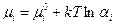, (4.7)

Активность компонента

,

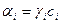где 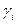- коэффициент активности.

Подставляя уравнение (4.7) в (4.3), получим

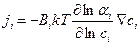. (4.8)

или

.

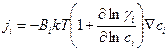Сравнивая полученное выражение с первым уравнением Фика, получаем выражение для коэффициента диффузии

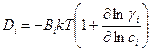. (4.9)

Уравнение (4.9) показывает, что коэффициент диффузии в реальном растворе зависит не только от кинетического фактора (подвижности), но и от термодинамического, каковым является коэффициент активности. Множитель в скобках в выражении (4.9) может приводить к диффузии против градиента концентрации, если 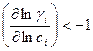. В этом случае имеет место так называемая восходящая диффузия.

Очевидно, выражение (4.8) описывает поток вещества под действием градиента концентрации и дополнительной движущей силы. В этом случае, первое уравнение Фика следует писать в виде

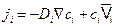. (4.10)

Поскольку средняя скорость, приобретаемая частицей под действием термодинамической силы 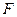равна 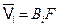, то из уравнения (4.8) и (4.10) следует, что в реальном растворе появляется добавочная сила

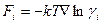. (4.11)

Эта сила передает влияние на поток градиента собственного потенциального поля, в котором движется диффундирующий атом. Такого градиента нет при самодиффузии. Им так же можно пренебречь в случае бесконечно разбавленного или совершенного растворов. Для неидеального раствора его влияние может быть существенным, поскольку в процессе диффузии окружение атома меняется и его взаимодействие со всем окружающими атомами нельзя считать одинаковым и, следовательно, его «эффективная» подвижность.

Таким образом эта движущая сила диффузии отличается от концентрационной. Это различие иллюстрирует рис.4.1, на котором сопоставлены слева - энергетическая диаграмма (зависимость энергии потенциального поля, в котором перемещается атом от координаты; точки 1 и 2 соответствуют двум соседним плоскостям решетки) и справа – концентрационная кривая (зависимость концентрации диффундирующего вещества от координаты; сплошная линия соответствует исходному распределению в момент времени 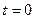, пунктирная ).

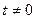В отсутствие внешних сил (рис. 4.1. а) барьер для скачка симметричен, поэтому энергия перемещения слева направо и в обратном направлении в среднем одна и та же. Одинаковы также вероятности и частоты таких переходов. Тем не менее, диффузионный поток возникает потому, что число атомов в плоскости 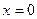больше, чем в любой другой, и уменьшается с уменьшением 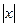- этому соответствует первый член в правой части уравнения (4.10). Концентрационная кривая симметрично размывается, но её максимум не смещается из нулевой точки.

Рис. 4.1 Энергетические диаграммы потенциальных барьеров и соответствующие им концентрационные кривые: а- без внешних сил; б – с внешними силами (1, 2 – узлы решетки)

Появление внешней силы приводит к нарушению симметрии барьера (рисунок 4.1 б). Вероятность перехода в направлении действия силы больше, чем в обратном. Симметрия концентрационной кривой нарушается, ее максимум сдвигается.

Второй член в правой части уравнения (4.10) описывает ещё и диффузию частиц при перемещении решетки как целого со скоростью 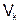. Этот случай был подробно рассмотрен в эффекте Киркендалла. Поскольку в этом случае добавочная скорость, которую приобретает частица любого сорта, постоянна для всех частиц, то иногда в уравнении (4.10) эту часть потока выделяют

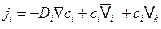, (4.12)