Термодинамика многокомпонентной системы при одновременном действии нескольких градиентов.

В качестве примера использования второго постулата Онзагера найдем термодинамические силы, вызывающие перенос вещества 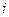-того сорта в многокомпонентной системе (так называемая химическая или диффузионная сила, 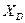) и перенос тепла (тепловая сила, 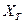) при одновременном действии градиентов концентрации и температуры.

Изменение энтропии при необратимом процессе записывается как

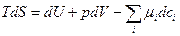, (4.16)

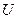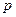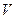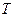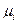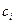здесь - внутренняя энергия; - давление; - объем; - температура; , и - химический потенциал и концентрация 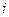-того компонента.

Если объем остается постоянным, а энергия и концентрация компонентов могут изменяться в связи с происходящим переносом тепла и вещества, выражение (4.16) примет вид

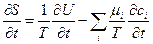. (4.17)

Частные производные берутся в произвольной точке системы.

Чтобы выразить 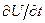и 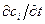через соответствующие плотности потоков энергии (тепла 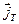) и вещества 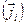, воспользуемся законами сохранения энергии:

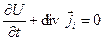(4.18)

и вещества (частиц 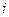-того сорта):

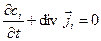, (4.19)

записанными в форме уравнений непрерывности.

Подставим 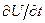и 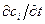из уравнений (4.18) и (4.19) в (4.17)

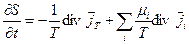. (4.20

Чтобы воспользоваться вторым постулатом Онзагера, нужно, чтобы правая часть уравнения (4.20) была записана в форме произведения потоков на градиенты, определяющие термодинамические силы ( 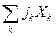). Заметим, что в правой части уравнения (4.20) стоят произведения скаляров на дивергенции векторов. Воспользуемся известным соотношением векторного анализа

,

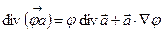следовательно,

.

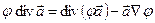тогда

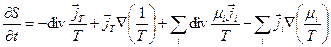или

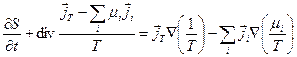. (4.21)

Видно, что правая часть уравнения (4.21) уже имеет нужную форму произведения потоков на градиенты. Левая же, очевидно, представляет собой полное изменение энтропии в единицу времени 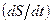, а выражение под знаком дивергенции имеет смысл плотности потока энтропии 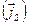в системе, где протекают потоки тепла 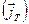и вещества :

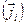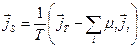. (4.22)

Таким образом, уравнение (4.21) совпадает по форме с уравнением (4.14) второго постулата Онзагера:

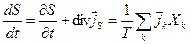. (4.23)

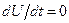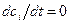Отметим, что для энтропии нет закона сохранения, как это есть для энергии или вещества: и , но .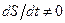

Из сравнения уравнений (4.23) и (4.21), видно, что тепловая сила

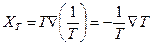, (4.24)

а диффузионная (химическая)

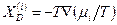. (4.25)

В изотермическом случае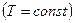

,

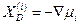что точно совпадает с результатом (4.2), полученным на основе качественного термодинамического анализа. Аналогично можно показать, что термодинамическая сила, вызывающая перемещение заряженной частицы в электрическом поле, равна

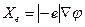, (4.26)

где 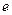- заряд частицы; 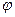- потенциал поля.

Термодинамическая сила химической реакции (роль «потока» в этом случае играет скорость реакции)

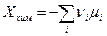, (4.27)

где 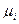- химический потенциал 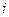-того компонента; 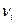- стехиометрический коэффициент 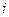-того компонента в уравнении реакции.

Поскольку в случае химической реакции «поток» является скалярной величиной, то и соответствующая сила — скаляр.

Исходя из полученных, результатов дадим общее феноменологическое описание изотермической диффузии в бинарной системе, содержащей атомы двух сортов и вакансии.

В системе возникнут три потока: два - атомов и третий - вакансий. В соответствии с первым постулатом Онзагера (4.13)

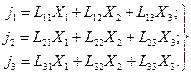(4.28)

Термодинамические силы, как это следует из уравнения (4.2), равны

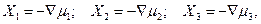(4.29)

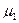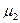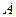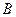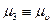где и - химические потенциалы атомов сортов и ; - химический потенциал вакансий.

Потоки (4.28) не являются независимыми. При вакансионном механизме диффузии, если объем образца не изменяется, сумма потоков должна быть равна нулю:

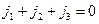, (4.30)

или поток вакансий

.

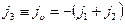Условие (4.30) выполняется при любых значениях 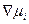, поэтому

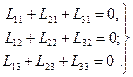(4.31)

С учетом выражения (4.31) и соотношений взаимности можно записать потоки атомов в следующем виде:

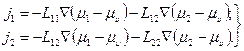(4.32)

Согласно первому уравнению Фика, любой из этих потоков имеет вид

.

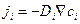Сравнение с уравнениями (4.32), полученными из общей феноменологической теории, позволяет сформулировать три условия применимости первого уравнения Фика.

1. Поток атомов любого сорта не зависит от градиента концентрации атомов другого сорта ( 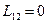). Первое уравнение Фика соответствует модели невзаимодействующих потоков атомов. Разумеется, потоки атомов и вакансий не являются независимыми.

2. Вакансия находится в равновесии: 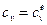, так что 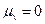. Достаточно и менее жесткого требования: концентрация вакансий всюду одинакова, тогда .

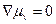3. Раствор - идеальный (бесконечно разбавленный или совершенный), так что химический потенциал обоих компонентов

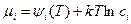и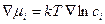

При выполнении этих условий оба уравнения (4.32) можно записать в виде

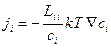(4.33)

и они совпадают с первым уравнением Фика, если

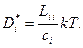(4.34)

Так как в разбавленном раствор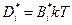е , где 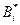- подвижность, то величина 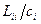имеет смысл подвижности атомов 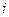-того сорта.

Отказ от третьего ограничения эквивалентен введению термодинамической активности. В реальном растворе 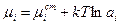. Подстановка этого выражения в уравнения для потоков опять приведет, в конечном счете, к первому уравнению Фика (4.9), но с коэффициентом диффузии

.

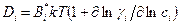Если потоки атомов взаимодействуют, то 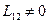. и полагая, кроме того, что

Если химические потенциалы компонентов связаны уравнениями Гиббса—Дюгема:

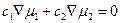, (4.35)

и сохраняется требование равновесия для вакансий и идеальности для раствора, то вместо уравнений (4.32) получим систему

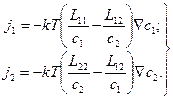(4.36)

Переход от уравнений (4.33) к уравнениям (4.36) эквивалентен учету вакансионного течения, которое полностью определяет величину перекрестного коэффициента 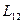. На важность эффекта вакансионного течения впервые указал Дж. Маннинг. Физически этот эффект заключается в следующем. Если атом движется по вакансионному механизму, то он может совершить, скачок только после того, как в ближайшем к нему узле появилась вакансия.

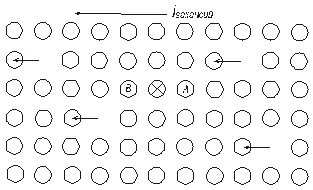
Рис. 4.2. Эффект течения вакансий

На рис. 4.2 поток вакансий направлен справа налево. При таком направлении потока вакансия имеет большую вероятность приблизиться к атому, показанному крестиком, справа в узел 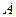, чем слева в узел 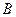. Поэтому выделенный атом будет, чаще совершать скачки вправо, чем влево. Величина эффекта зависит от того, насколько часто вакансии приближаются к данному атому по различным направлениям. Таким образом, она зависит от частоты скачков других атомов, а не выделенного атома.

Эффект течения вакансий отличен от эффекта корреляции. Появление корреляционного множителя обусловлено тем, что скачки рассматриваемого атома влияют на распределение вакансий, находящихся вблизи от него. Фактор корреляции не изменяется, если приложена движущая сила. Наоборот, эффект течения вакансий зависит от того, как изменяется распределение вакансий вблизи данного атома из-за движения других атомов, а не его. Этот эффект пропорционален движущей силе и исчезает при стремлении потока вакансий к нулю.

Маннинг показал, что учет вакансионного течения заметно изменяет коэффициент взаимной диффузии и сдвиг меток в эффекте Киркендалла.

Таким образом, даже в простом случае бинарного сплава учет перекрестных коэффициентов может быть существенным.

Положение еще более усложняется в многокомпонентных системах, в которых число независимых коэффициентов 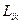даже с учетом соотношений взаимности составляет 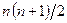, где 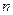— число компонентов. Пренебрегать перекрестными коэффициентами в большинстве случаев нельзя, поскольку взаимодействие компонентов является существенным.