Диффузия под действием поверхностного натяжения

Существует множество металлургических процессов, в которых движущей силой диффузии является поверхностное натяжение или поверхностная свободная энергия твердых тел. Например, при спекании чистых металлических порошков понижение свободной энергии связано с большим уменьшением поверхности раздела между твердым телом и паром.. Принципы расчета скорости каждого из этих процессов известны. Однако геометрические трудности делают такие расчеты в действительности весьма сложными.

Рассмотрим образование под действием поверхностного натяжения на поверхности металла по границе зерна канавок травления. Анализируемая система представляет собой металлический бикристалл с плоской границей, перпендикулярной поверхности. Сечение образца по нормали к границам и поверхности показано на рис. 3.9, а. Поверхностное натяжение (свободная энергия поверхности) стремится уменьшить величину поверхности. Поэтому при выходе границы на внешнюю поверхность она будет сжиматься по оси 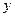до тех пор пока поверхностное натяжение границы 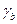не уравновесит поверхностное натяжение двух прилегающих поверхностей раздела твердое тело - пар, 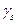. Это локальное равновесие достигается, если

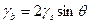(3.17)

где 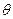— угол между касательными к внешней поверхности в вершине канавки и вдали от нее (рис. 3.9., а).

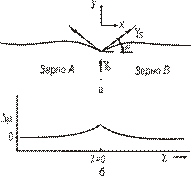
Рис. 3.9. Нормальное (к поверхности) сечение бикристалла. На границе канавка а; химический потенциал атомов в различных точках поверхности (в соответствии с верхним рисунком) б

Канавка искривляет плоскую поверхность. Атомы в области, имеющей радиус кривизны 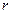, обладают более высоким химическим потенциалом, чем на плоскости при равных давлении и температуре. Разность химических потенциалов дается уравнением Гиббса — Томсона:

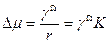,(3.18)

где 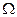- атомный объем; 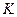- кривизна поверхности.

Точное выражение для 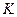имеет вид

,

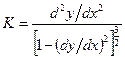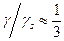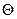но поскольку и - маленький угол, то 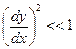, поэтому 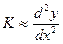и приближенно

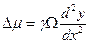. (3.19)

На рис. 3.9 б показан химический потенциал атомов на поверхности в зависимости от 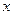. Величина 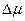, достигает максимума при 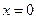и уменьшается по обе стороны от этого значения. Это уменьшение означает, что градиент 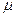не равен нулю и он вызывает уход атомов от границы вдоль поверхности. Возникающий поток приводит к уширению и углублению канавки.

Для определения скорости роста канавки следовало бы написать уравнение для потока. Однако атомы могут уходить от границы несколькими путями: диффундируя по поверхности кристалла, по его объему или через паровую фазу. Оценим относительный вклад указанных трех процессов. Любой поток вдоль оси 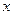есть произведение средней скорости атомов под действием единичной силы (разной для разных путей и равной 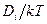) на плотность атомов 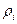и среднюю силу, действующую на атом - 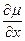. Таким образом, поток

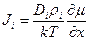. (3.20)

Суммарное количество вещества, переносимого по каждому пути в единицу времени, равно потоку, умноженному на соответствующее эффективное сечение. Тогда относительный вклад поверхностной и объемной диффузии равен

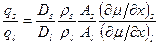. (3.21)

Если принять, что плотность вещества на поверхности и в объеме совпадает, то

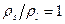. Поверхностная диффузия происходит в слое толщиной 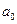(аналог 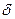для пограничной диффузии), так что на единицу длины параллельно канавке сечение 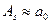. В случае объемной диффузии существует множество возможных путей между любыми двумя точками на поверхности. Некоторые из них схематически показаны на рис. 3.10.

Рис. 3.10. Схема, указывающая на многочисленность путей, пригодных для перехода атомов внутри кристалла из одной точки его поверхности в другую

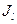Чем глубже путь проходит внутри кристалла, тем меньше его вклад в . Предположим, что одинаков для всех путей до глубины, равной ширине канавки 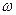, а для более глубоких . Считая 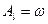и принимая 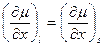, получим

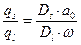. (3.22)

Если вначале поверхность была плоской, то 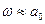, а так как 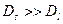, то и 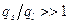. Однако в процессе диффузии величина 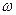растет и, если считать 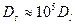, то когда 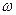вырастает примерно до 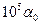, вещество переносится по обоим путям с одинаковой скоростью.

Рассмотрим теперь роль переноса через газовую фазу в процессе образования пограничной канавки. Если отжиг проводили в инертном газе, то средняя длина свободного пробега в газовой фазе гораздо меньше, чем 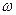. Ко всем остальным величинам применимы те же рассуждения, что и в предыдущем случае, только 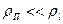. Поэтому вместо выражения (3.22) имеем

.

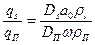Если канавка узкая, то скорость роста контролируется поверхностной диффузией. Для широких канавок может преобладать другой механизм: диффузия через пар или объемная диффузия в зависимости от отношения .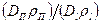

Рассчитаем теперь скорость роста пограничной канавки, если все вещество переносится с помощью поверхностной диффузии. Поток поверхностной диффузии в атомах на квадратный сантиметр в секунду по формуле (3.20) равен:

,

где 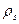заменено обратной величиной атомного объема . Эта формула аналогична формуле (3.2), в которой определяется 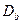. Если рассмотреть элемент поверхности шириной 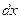, имеющий единичную длину в направлении вершины канавки, то количество приходящего в него вещества пропорционально

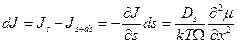. (3.23)

Накопление вещества создает бугорок на поверхности, так что 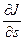пропорционально скорости поднятия поверхности 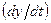. Чтобы получить точное равенство вместо пропорциональности, надо ввести эффективную глубину поверхностного слоя, обладающего высокой скоростью диффузии, как было сделано для пограничной диффузии. Если обозначить эту глубину через 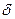, то число атомов, попадающих в секунду в элемент поверхности, равно 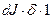, а скорость поднятия элемента поверхности равна приращению объема этого участка в секунду, т. е.

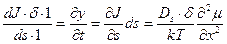. (3.24)

Используя выражение (3.19), получим

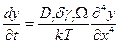. (3.25)

В случае образования канавки на границе Муллинс ввел следующие граничные условия:

1. Поверхность вначале плоская, т. е. 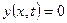при .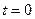

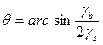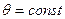2. Равновесное значение угла и при ,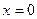

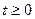
3. 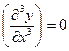для всех , т. е. поток атомов от границы отсутствует.

Решение уравнения (3.25) при этих условиях имеет следующий вид:

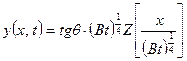, (3.26)

где 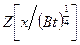— степенной ряд, а

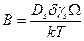(3.27)

и 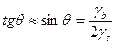. Из данного решения следуют два свойства канавок:

1. форма канавки заданного профиля не зависит от времени;

2. все линейные размеры канавки пропорциональны .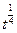

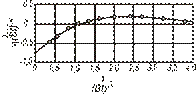
Рис. 3.11. Профиль поверхности с канавкой на границе, если контролирующий процесс – поверхностная диффузия. Кривая построена по уравнению

Сплошная кривая на рис. 3.11 показывает форму канавки (точки взяты из опыта с медью). Тот факт, что эта кривая справедлива для любого времени, означает, что координаты 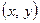данной точки канавки растут одинаково, как .

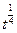Особенно существенно, что расстояние между двумя максимумами по обе стороны границы (т. е. ширина канавки, 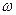) и глубина (расстояние от максимума до вершины канавки, 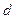) растут, как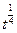

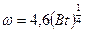, (3.28)

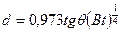. (3.29)

Два максимума по обе стороны границы возникают потому, что вещество не уходит из области 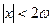. Поэтому в процессе роста канавки уровень металла на границе становится ниже исходного, а по обе стороны границы возникают широкие максимумы. Они возникали бы и в случае преобладания другого механизма переноса (объемной диффузии, переноса через газовую фазу), если только нет потери вещества. Однако в этом случае ширина канавки (расстояние между, максимумами) росла бы как 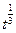, а не .

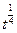3.5 Определение 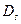методом канавок травления

Для меди все величины, входящие в выражение для 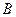[формула (3.27)], известны, кроме 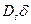. Поэтому если форма канавок и увеличение их размера во времени подчиняются уравнению (3.26), измеряя 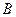, можно найти 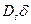. Точки на рис. 3.11 получены для меди, отожженной в сухом водороде. Они показывают, что форма канавки удовлетворительно описывается уравнением (3.26).

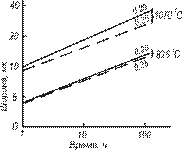
Рис. 3.12. Зависимость ширины медных канавок от времени для различных температур. Для каждой температуры сплошная линия соответствует наблюдаемой ширине, а штриховая – доле поверхностной диффузии в ней. Цифра у каждой линии означает ее наклон

На рис. 3.12 построена зависимость ширины канавки от времени. Цифра, написанная около каждой прямой - её наклон и, следовательно, показатель степени у . Эксперимент показывает, что при относительно высоких температурах и для сравнительно широких канавок наклон линий, проведенных по опытным точкам, несколько больше 0,25. Однако, если вычесть вклад объемной диффузии, наклон результирующих прямых (штрихи на рис. 3.11) равен 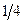. Принимая 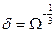или примерно равным атомному диаметру, для меди можно написать:

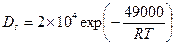см²/сек.

Для всех изученных поверхностей величина 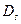меняется не более чем в три раза, так что написанное выражение справедливо для любой ориентации поверхности.

Энергия активации поверхностной самодиффузии 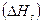меди почти равна объемной 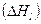. Столь большая величина 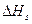может вначале показаться странной, так как перемещение атома вдоль поверхности не требует деформации объема. Однако атом, перескакивающий вдоль поверхности, каждый раз как бы претерпевает процесс испарения. Поэтому значение 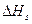должно быть теснее связанным с теплотой испарения металла, чем с 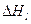. Теплота испарения меди 333 кдж/моль (80 ккал/моль). Если предположить, что энергия связи атома меди пропорциональна числу ближайших соседей, то можно показать, что 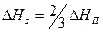для металла с гцк решеткой. Отсюда следует, что для меди 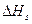равняется примерно 222,5 кдж/моль (53 ккал/моль). Из этой модели следует также, что 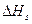должно иметь одинаковую величину независимо от ориентации поверхности. И то и другое удовлетворительно согласуется с экспериментом.

3.6. Определение 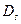из эмиссионных опытов

Для изучения поверхностной диффузии успешно применяли также метод, основанный на использовании эмиссионного микроскопа. В нем очень сильное поле приложено к заостренной металлической проволоке (радиус кривизны от 0,1 до l,0 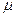). В высоком вакууме острие эмитирует электроны — процесс можно наблюдать с помощью фосфоресцирующего экрана. С помощью этого метода были выполнены эксперименты двух типов.

Во-первых, скругление металлического острия при 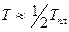контролируется диффузией и по скорости скругления можно определить 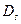. Для вольфрама:

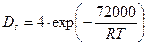см²/сек.

Одно из основных преимуществ этого метода - возможность получения чистой поверхности. Число металлов, с которыми удобно работать, незначительно, но оно ограничивается факторами, отличающимися от ограничивающих факторов в методе канавок травления, так что оба метода дополняют друг друга.

В опытах второго типа на одной стороне металлического острия хемсорбируется растворенное вещество, например кислород на вольфраме. Оно локально изменяет работу выхода, в связи с чем изменяется и картина электронной эмиссии. Изучение этой картины позволяет судить о скорости растекания растворенного вещества вдоль поверхности металла. Таким образом, можно определить энергию активации поверхностной диффузии и наблюдать изменение коэффициента диффузии в зависимости от ориентации поверхности