Процессы диффузионного роста фаз
Задачи, связанные с ростом новой фазы, возникают при распаде пересыщенных твердых растворов, диффузионном насыщении металла легирующим элементом, если концентрация последнего превосходит предел растворимости, и во многих других случаях, важных для практики термической и химико-термической, обработки. Характерная особенность происходящих при этом процессов заключается в сочетании диффузии с фазовыми превращениями или образованием химических соединений. При диффузии атомы перемещаются на расстояния, намного превосходящие межатомные, а при фазовом или химическом превращении процесс происходит на границе раздела фаз.
Фактически возникающие задачи относятся к проблемам гетерогенной кинетики, так как происходящий процесс многостадиен и включает в себя, как минимум, перестройку решетки (химическую реакцию) на границе раздела фаз и диффузионный подвод-отвод растворенного вещества, если состав возникающей фазы отличается от исходной. Однако обычно считают, что перестройка происходит быстро (отсутствуют кинетические затруднения), и скорость процесса контролируется диффузией. В этом случае процесс роста частиц новой фазы является чисто диффузионным.
Кроме того, часто считают, что атомы растворенного вещества движутся в практически неподвижной решетке растворителя, и вводят в расчет коэффициент диффузии этих атомов в данной фазе, а не коэффициент взаимной диффузии, который чаще всего неизвестен. Возможность такого упрощения задачи фактически вытекает из уравнения 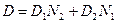 ; при
; при 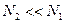
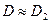 . Для твердых растворов внедрения, например для системы
. Для твердых растворов внедрения, например для системы 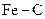 , кроме того,
, кроме того, 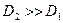 .
.
Для определения скорости роста составляют уравнение баланса вещества на движущейся поверхности раздела фаз. При отыскании формы поверхности раздела возникают большие математические трудности, поэтому в простых случаях её задают; чаще всего эту поверхность принимают плоской или сферической.
|
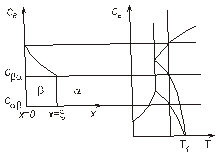
Рис. 5.3. Схема роста  -фазы в двухфазном ( -фазы в двухфазном (  ) сплаве при температуре ) сплаве при температуре 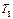 показанной вертикальной пунктирной линией показанной вертикальной пунктирной линией
|
Рассмотрим в качестве примера решенную Вагнером задачу о росте 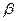 -фазы, в двухфазном (
-фазы, в двухфазном ( 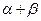 ) сплаве. В соответствии с условиями задачи на поверхности образца поддерживается концентрация компонента
) сплаве. В соответствии с условиями задачи на поверхности образца поддерживается концентрация компонента 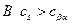 , а концентрация внутри образца в начальный момент времени
, а концентрация внутри образца в начальный момент времени 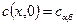 (рис. 5.3). Вагнер принимает, что на плоской границе растущей фазы концентрация скачком изменяется от равновесной в
(рис. 5.3). Вагнер принимает, что на плоской границе растущей фазы концентрация скачком изменяется от равновесной в 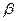 -фазе (
-фазе ( 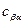 ) до равновесной в
) до равновесной в 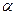 -фазе (
-фазе ( 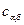 ) при температуре
) при температуре 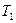 , иначе говоря, его теория справедлива для случая, когда скорость диффузии мала по сравнению со скоростью фазового превращения. Коэффициент диффузии в пределах
, иначе говоря, его теория справедлива для случая, когда скорость диффузии мала по сравнению со скоростью фазового превращения. Коэффициент диффузии в пределах 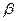 -фазы (
-фазы ( 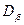 ) не зависит от концентрации.
) не зависит от концентрации.
Граница растущей 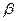 -фазы смещается пропорционально корню квадратному из времени:
-фазы смещается пропорционально корню квадратному из времени:
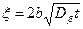 . (5.2)
. (5.2)
Для определения 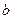 мы располагаем двумя уравнениями. Первое описывает распределение концентрации в
мы располагаем двумя уравнениями. Первое описывает распределение концентрации в 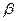 -фазе (
-фазе ( 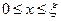 ):
):
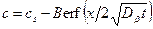 . (5.3)
. (5.3)
Коэффициент 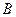 легко найти из граничного условия
легко найти из граничного условия 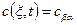 .
.
Второе уравнение баланса - скорость роста фазы определяется количеством подводимого к ней вещества:
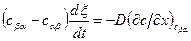 . (5.4)
. (5.4)
Находим из уравнения (5.2) 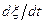 , а из уравнения (5.3)
, а из уравнения (5.3) 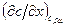 и подставляя их в уравнение (5.4), получим
и подставляя их в уравнение (5.4), получим
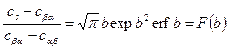 . (5.5)
. (5.5)
В таблице приведены значения 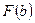 для различных
для различных 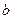 . Зная левую часть уравнения (5.5), находят
. Зная левую часть уравнения (5.5), находят 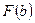 , затем
, затем 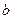 . Тогда уравнение (5.2) позволяет рассчитать
. Тогда уравнение (5.2) позволяет рассчитать 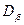 , если известна скорость роста фазы, и, наоборот, найти эту скорость, если известен коэффициент диффузии.
, если известна скорость роста фазы, и, наоборот, найти эту скорость, если известен коэффициент диффузии.
При малых значениях 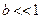 можно разложить функцию
можно разложить функцию 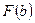 в ряд и ограничиться первыми членами разложения
в ряд и ограничиться первыми членами разложения 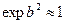 и
и 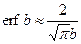 . Тогда
. Тогда
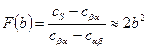 . (5.6)
. (5.6)
Подставляя уравнение (5.6) в (5.2), получим
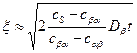 . (5.7)
. (5.7)
Значения 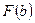
| |||||||
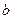
| 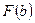
| 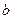
| 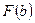
| 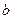
| 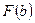
| 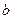
| 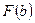
|
| 0,40 | 0,3564 | 0,80 | 1,9955 | 1,20 | 8,1900 | ||
| 0,04 | 0,0032 | 0,44 | 0,4412 | 0,84 | 2,3067 | 1,22 | 8,7696 |
| 0,08 | 0,0129 | 0,48 | 0,5385 | 0,88 | 2,6613 | 1,24 | 9,4138 |
| 0,12 | 0,0291 | 0,52 | 0,6497 | 0,92 | 3,0670 | 1,26 | 10,1076 |
| 0,16 | 0,0521 | 0,56 | 0,7763 | 0,96 | 3,5297 | 1,28 | 10,8556 |
| 0,20 | 0,0822 | 0,60 | 0,9205 | 1,00 | 4,0599 | 1,30 | 11,6622 |
| 0,24 | 0,1197 | 0,64 | 1,0842 | 1,04 | 4,6569 | 1,32 | 12,5338 |
| 0,28 | 0,1653 | 0,68 | 1,2704 | 1,08 | 5,3664 | 1,34 | 13,4728 |
| 0,32 | 0,2193 | 0,72 | 1,4817 | 1,12 | 6,1714 | 1,36 | 14,4904 |
| 0,36 | 0,2828 | 0,76 | 1,7200 | 1,16 | 7,6994 | 1,38 | 15,5874 |
Вагнер решил в таком же приближении целый ряд задач. Например, если исходным является однофазный сплав 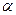 , то диффузия происходит как в
, то диффузия происходит как в 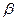 -фазе, так и в
-фазе, так и в 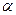 -фазе, и распределение концентраций в каждой из фаз характеризуется своим коэффициентом
-фазе, и распределение концентраций в каждой из фаз характеризуется своим коэффициентом 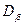 и
и 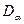 .
.
По-прежнему 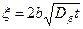 .
.
Уравнение баланса имеет вид
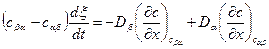 . (5.8)
. (5.8)
Коэффициент 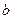 находят из уравнения
находят из уравнения
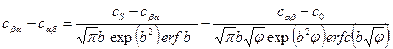 (5.9)
(5.9)
где 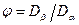 . Зная один из коэффициентов, можно найти другой или, зная оба, найти скорость роста фазы.
. Зная один из коэффициентов, можно найти другой или, зная оба, найти скорость роста фазы.
Б. Я. Любов учел, что при малых временах концентрация на поверхности раздела фаз отличается от равновесного значения 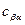 , т. е. ввел пересыщение в растущей
, т. е. ввел пересыщение в растущей 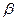 -фазе, а А. А. Жуховицкий и др. ввели пересыщение как в
-фазе, а А. А. Жуховицкий и др. ввели пересыщение как в 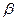 -, так и в
-, так и в 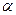 -фазах. Таким образом,
-фазах. Таким образом, 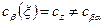 и
и 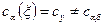 . С увеличением времени диффузионного отжига
. С увеличением времени диффузионного отжига 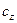 и
и 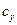 стремятся к равновесным значениям
стремятся к равновесным значениям 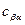 и
и 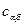 . При этом пересыщение пропадает, теория Вагнера справедлива.
. При этом пересыщение пропадает, теория Вагнера справедлива.
В случае, когда значения 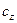 и
и 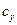 не являются равновесными, следует учитывать скорость химической реакции (фазового превращения)
не являются равновесными, следует учитывать скорость химической реакции (фазового превращения) 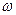 ; все авторы считали, что она подчиняется кинетическому уравнению первого порядка:
; все авторы считали, что она подчиняется кинетическому уравнению первого порядка:
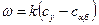 , (5.10)
, (5.10)
где 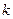 — константа скорости.
— константа скорости.
В работе А. А. Жуховицкого и др. было принято, что, несмотря на нестабильность исчезающей фазы, на границе раздела имеется равновесие в отношении перехода компонента 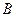 . Иначе говоря, хотя
. Иначе говоря, хотя 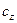 и
и 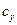 не равны равновесным значениям, однако их отношение такое же, как в равновесии:
не равны равновесным значениям, однако их отношение такое же, как в равновесии:
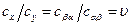 . (5.11)
. (5.11)
С учетом этих предположений было получено решение, которое можно представить в виде ряда. Результат Вагнера является первым членом ряда:
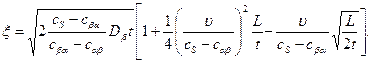 (5.12)
(5.12)
Здесь 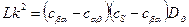
Если ограничиться вторым членом разложения, то
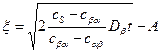 , (5.13)
, (5.13)
где 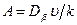 .
.
Естественно, что учет кинетических затруднений приводит к уменьшению толщины слоя 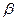 -фазы по сравнению с теорией Вагнера. Величина отклонения от теории Вагнера тем больше, чем меньше константа скорости
-фазы по сравнению с теорией Вагнера. Величина отклонения от теории Вагнера тем больше, чем меньше константа скорости 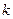 и чем больше скорость диффузии
и чем больше скорость диффузии 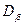 .
.
ЗАКЛЮЧЕНИЕ
Учебное пособие содержит основные сведения о процессах массопереноса в твёрдых кристаллических телах. В книге подробно рассмотрены феноменологические уравнения диффузии, основанные на фундаментальных законах Фика. Подробно описана проблема случайных блужданий атомов и основные механизмы диффузии в периодической кристаллической решётке. Последовательно изложены термодинамические основы диффузии и диффузия в многофазных системах.
В результате изучения изложенного материала студент должен знать основы процессов диффузионного массопереноса в кристаллических твёрдых телах.
Учебное пособие восполняет имеющийся недостаток учебной литературы по диффузии и будет полезно для студентов и аспирантов, специализирующихся в области физического материаловедения.
Дата добавления: 2020-07-18; просмотров: 888;











