В.2 Момент сопротивления повороту и сила тяги на гусеницах.
Пренебрегая центробежной силой, действующей на мобот при повороте и полагая, что поворот происходит на горизонтальной площадке, представим схему внешних сил. В этом случае к каждой гусеничной цепи приложены: сила тяги Р1 (для отстающей цепи) или Р2 (для забегающей цепи), сила сопротивления прямолинейному движению 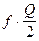 и поперечные силы, образующие момент сопротивления повороту МС (рис. 13). Допустим, что полюсы поворота цепей О1 и О2 находятся на поперечной оси машины, удельное давление по длине цепей одинаковое, коэффициент сопротивления повороту m постоянный и поворот осуществляется с постоянным, заранее заданным радиусом. Считаем также, что ширина гусеничной цепи настолько мала, что ею можно пренебречь, тогда величина q будет означать удельное давление, приходящееся на единицу длины цепи:
и поперечные силы, образующие момент сопротивления повороту МС (рис. 13). Допустим, что полюсы поворота цепей О1 и О2 находятся на поперечной оси машины, удельное давление по длине цепей одинаковое, коэффициент сопротивления повороту m постоянный и поворот осуществляется с постоянным, заранее заданным радиусом. Считаем также, что ширина гусеничной цепи настолько мала, что ею можно пренебречь, тогда величина q будет означать удельное давление, приходящееся на единицу длины цепи:
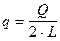 ( 49 )
( 49 )
Поскольку поворот происходит на горизонтальной площадке, нормальная реакция грунта RZ равна весу машины G.
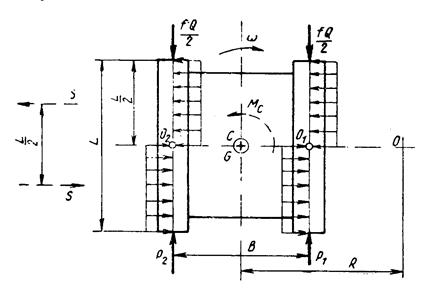
Рис. 14. Схема внешних сил, действующих на машину при её повороте.
Эпюры поперечных сил можно представить в виде прямоугольников, равнодействующие этих сил определяются по формуле:
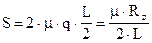
Момент сопротивления повороту двух гусеничных цепей найдём по зависимости:
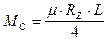 ( 50 )
( 50 )
Для осуществления поворота необходимо знать потребные силы тяги Р1 и Р2. Спроецируем все действующие силы на продольную ось машины:
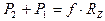 ( 51 )
( 51 )
Уравнение моментов сил относительно центра машины имеет вид
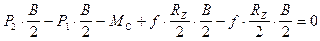 ,
,
откуда
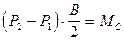 ( 52 )
( 52 )
Используя выражения (50) и (51), можно написать:
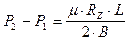 ( 53 )
( 53 )
После совместного решения формул (51) и (53) получим:
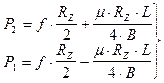 ( 54 )
( 54 )
Из уравнений (54) видно, что сила тяги на забегающей гусеничной цепи больше, чем на отстающей на величину 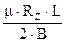 . Кроме того, из соотношений (51) и (53) видно, что с уменьшением силы тяги на отстающей цепи сила тяги на забегающей цепи возрастает на такую же величину и, следовательно, соотношение сил Р1 и Р2 определяется величиной коэффициента сопротивления повороту m.
. Кроме того, из соотношений (51) и (53) видно, что с уменьшением силы тяги на отстающей цепи сила тяги на забегающей цепи возрастает на такую же величину и, следовательно, соотношение сил Р1 и Р2 определяется величиной коэффициента сопротивления повороту m.
Зависимость (52) показывает, что момент, поворачивающий мобот, равен моменту сопротивления повороту. Увеличение момента МС вызывается ростом коэффициента m и может оказаться, что для выполнения поворота увеличить поворачивающий момент можно только изменением силы тяги Р1, что осуществляется торможением отстающей гусеничной цепи.
Итак, для равномерного поворота мобота на забегающей и отстающей гусеничных цепях двигатель и трансмиссия или механизм поворота, должны обеспечить приложение потребных сил тяги Р2 и Р1, определяемых уравнениями (54). Мощность, потребная для поворота, всегда больше мощности прямолинейного движения, хотя сумма сил тяги при повороте равна силе тяги прямолинейного движения (см. формулу (51)).
Из уравнения (50) видно, что для данного мобота момент МС определяется коэффициентом сопротивления повороту m, который зависит от трения поверхностей траков о грунт, смятия и среза грунта траками и от сопротивления рыхлого грунта, нагребаемого гусеницей и катками и радиуса поворота скольжения S, имеющего сложную природу
Справочные величины максимального коэффициента сопротивления повороту mmax представлены в таблице Т3.
Таблица Т3
| Стальная гусеница по бетону | 0,35 ... 0,45 |
| Сухая грунтовая дорога на суглинке | 0,7 ... 0,9 |
| Суглинистая влажная дорога | 0,3 ... 0,4 |
| Снег рыхлый | 0,25 ... 0,30 |
| Снег, слежавшийся при температуре 0°С | 0,6 ... 0,7 |
Для определения текущих значений m достаточно воспользоваться эмпирической зависимостью коэффициента сопротивления повороту от радиуса поворота:
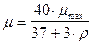 ( 55 )
( 55 )
Формула (55) свидетельствует об уменьшении коэффициента m с увеличением радиуса поворота. Для прямолинейного движения, когда r стремится к бесконечности, m стремится к нулю. В этом случае силы тяги Р2 и Р1 соответствуют прямолинейному движению (см. уравнение (54)).
Дата добавления: 2020-04-12; просмотров: 1087;











