Связь между характеристиками диффузии и диаграммами фазового равновесия

Если диффузия происходит в гомогенном твердом растворе, то концентрационные кривые имеют плавный вид. Если система состоит из нескольких фаз, то на концентрационных кривых 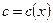появляются вертикальные ступеньки, обусловленные тем, что гетерогенные смеси не могут образоваться диффузионным путем. Действительно, в пределах двухфазной области составы соответствующих фаз постоянны, и градиент концентрации в пределах каждой из них равен нулю. Фаза может расти в результате диффузии только в том случае, если ей отвечает на диаграмме область гомогенности, внутри которой может возникнуть градиент концентрации.

Соответственно диффузия через стехиометрическое химическое соединение, строго говоря, невозможна, если перенос вещества, происходит только под действием градиента концентрации. Это правило, обычно не выполняется, так как всегда имеется хотя бы небольшая область растворимости или действуют другие градиенты.

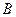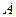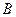Это иллюстрируется рис. 5.1. Нижний рисунок в каждой паре представляет собой повернутую на 90° концентрационную кривую, описывающую диффузию компонента в образце, составленном из двух металлов и . Очевидно, что высота (ширина на рис. 5.1.) ступеньки соответствует ширине двухфазной области на диаграмме.

Рис. 5.1. Концентрационные кривые для взаимной диффузии в бинарных сплавах: а — неограниченная растворимость; б — двухфазная область ; горизонтальной пунктирной линией показана плоскость Матано; в — две двухфазные области и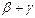

Если вещество 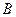диффундирует при температуре в 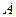, то у поверхности раздела образуется фаза 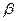. В любой момент времени ( 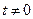) концентрация компонента 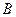в фазе 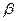изменяется от 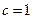(атомные доли) на поверхности до 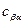, отвечающего пределу растворимости 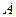в 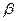при этой температуре. На границе растущей фазы 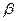образуется новая фаза, концентрация вещества в которой изменяется от 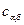до нуля.

Если фаза образуется быстро, так что кинетика роста фазы является диффузионной, то толщина фазы увеличивается пропорционально корню квадратному из времени. Поэтому если 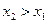в два раза, как это изображено на рис. 5.2, то 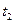больше 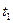в четыре раза.

Рис. 5.2. Движение ступеньки в двухфазной области

Для расчета коэффициентов диффузии в многофазной системе в принципе можно пользоваться методом Матано, если известна зависимость 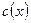. Очевидно, скорость роста фазы будет зависеть не только от коэффициента диффузии в ней, но и от ширины области растворимости.

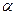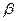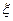Применим, например, метод Матано к границе раздела фаз и , изображенной на рис. 5.1. б. Пусть горизонтальная пунктирная линия соответствует плоскости Матано. Расстояние от плоскости Матано до границы раздела обозначим через . Тогда в соответствии с уравнением (1.73)

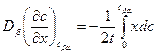
и

.

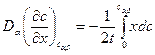Откуда

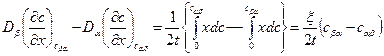(5.1)

Очевидно, величина 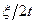характеризует скорость роста фазы. Действительно, если 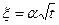, то 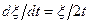. Эта скорость тем больше, чем больше коэффициент диффузии в данной фазе ( 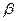) по сравнению с соседней ( 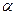), т.е 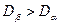. Она зависит от ширины этой области и от того, насколько резко изменяется концентрация на границах двухфазной области ( ). Таким образом, фаза, растущая с наибольшей скоростью, не всегда характеризуется наибольшим коэффициентом диффузии.

На основе анализа экспериментальных данных по росту фаз при взаимной диффузии были сформулированы следующие правила. Скорость роста фазы тем больше:

1) чем больше коэффициент диффузии в этой фазе по сравнению с соседней;

2) чем уже прилегающая к данной фазе двухфазная область;

3) чем шире область гомогенности данной фазы.

Видно, что все три правила фактически следуют из уравнения (5.1).

На концентрационных кривых может не быть области, соответствующей одной из фаз, имеющихся в системе (например, 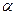-твердого раствора). Это означает пренебрежимо малую скорость роста 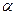-фазы по сравнению с 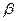-фазой. В условиях, когда процесс образования фазы происходит быстро и концентрации на краях ступеньки соответствуют равновесным (по диаграмме), область 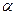-фазы не наблюдается, если выполняется условие , где 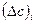— ширина области гомогенности 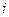-той фазы.