Диффузия в твердых растворах внедрения
Межузельный механизм является основным механизмом перемещения примесных атомов небольшого размера, образующих твердые растворы внедрения в металлах с плотноупакованной решеткой.
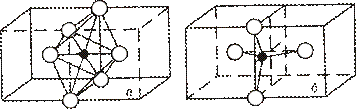
В металлах с оцк решеткой имеются два типа междоузлий. Первый тип – октапоры, центры которых находятся на середине ребер или в центре граней куба (рис. 2.12, а), и второй - тетрапоры (рис. 2.12, б). Внедренные атомы занимают, как правило, октапоры.
Атом в октапоре имеет двух соседей по направлению [100] на расстоянии 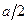 и четырех - в перпендикулярной плоскости на расстоянии
и четырех - в перпендикулярной плоскости на расстоянии 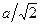 . Таким образом, искажение, вызываемое внедренным атомом, по оси
. Таким образом, искажение, вызываемое внедренным атомом, по оси 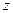 [100] больше, чем по
[100] больше, чем по 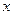 и
и 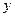 .
.
|
| Рис. 2.12. Окта (а) и тетра (б) положения внедренного атома в кристалле с оцк решеткой |
Если приложить к кристаллу растягивающее напряжение по одной из осей, то первоначальная равномерная заселенность 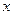 ,
, 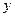 и
и 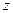 положений нарушается и при этом возникает дополнительная упругая деформация. Это дополнительное деформирование представляет собой не мгновенный, а длительный релаксационный процесс, протяженность которого (время релаксации
положений нарушается и при этом возникает дополнительная упругая деформация. Это дополнительное деформирование представляет собой не мгновенный, а длительный релаксационный процесс, протяженность которого (время релаксации 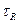 ) определяется частотой диффузионных скачков атома (
) определяется частотой диффузионных скачков атома ( 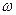 ). Можно показать, что в оцк решетке
). Можно показать, что в оцк решетке 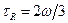 и
и 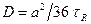 .
.
В табл. 2.3 приведены результаты определения этим методом параметров диффузии некоторых примесей внедрения в металлах с оцк решеткой. Как видно из таблицы, энергия активации межузельной диффузии составляет всюду около 1/3 энергии активации самодиффузии, т. е. несколько меньше энергии перемещения вакансии. Предэкспоненциальный фактор так же несколько меньше, чем при вакансионном механизме.
| Таблица 2.3 Параметры диффузии примесей внедрения | |||||||
| Внедренный атом | 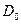 , см2/с , см2/с
| 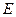 , ккал/г-атом , ккал/г-атом
| 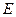 *, ккал/г-атом *, ккал/г-атом
| Внедренный атом | 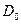 , см2/с , см2/с
| 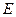 , ккал/г-атом , ккал/г-атом
| 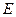 *, ккал/г-атом *, ккал/г-атом
|
| 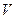
| ||||||
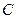
| 0,02 | 20,1 | 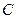
| 0,005 | 33,0 | ||
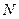
| 0,0066 | 18,6 | 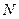
| 0,009 | 34,9 | ||
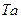
| 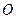
| 0,01 | 26,9 | ||||
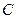
| 0,006 | 38,5 | 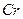
| ||||
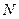
| 0,006 | 33,0 | 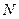
| 0,01 | 28,5 | 53-73 | |
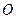
| 0,004 | 25,5 | 3×10-4 | 24,3 | |||
| 3,5×10-6 | 20,5 | ||||||
| * Самодиффузия растворителя |
С увеличением размера внедренных атомов возрастает энергия активации. Это хорошо видно из данных, представленных в табл. 2.4 для примесей внедрения в 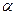 -железе.
-железе.
Таблица 2.4
Связь между энергией активации диффузии внедренных атомов в 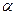 -железе и их размером -железе и их размером
| |||
| Внедренный атом | Радиус, 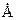
| 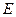 , ккал/г-атом , ккал/г-атом
| |
| ковалентный | ионный | ||
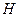
| 0,28 | 0,00(1+) | 2,9 |
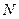
| 0,70 | 0,11(5+) | 18,2 |
| 0,13-0,16(3+) | |||
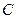
| 0,77 | 0,15(4+) | 20,1 |
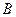
| 0,83 | 0,20(3+) | 20,3 |
| Примечание. В скобках указано зарядовое состояние иона |
В кристаллах с гцк решеткой также имеются два сорта междоузлий: октапоры, расположенные в центре куба и середине ребра, и тетрапоры типа, расположенные на 1/4 диагонали куба. Все они симметричны и не дают упругого последействия, но оно все же может возникать, если образуются пары типа атом внедрения - примесный атом замещения или два атома внедрения.
При классическом описании диффузии мы всегда принимаем, что атом в узле решетки совершает малые колебания около положения равновесия; амплитуды колебаний намного меньше периода решетки. Точно так же дефекты (вакансии, межузельные атомы) классически рассматривают как локализованные объекты, лишь изредка перемещающиеся из одного положения в другое, преодолевая барьер. Это описание фактически считается справедливым при любых температурах, вплоть до 0 К.
Оказалось, однако, что существуют такие кристаллы, для которых амплитуда нулевых колебаний, т. е. колебаний, которые остаются при нуле температуры, не мала по сравнению с периодом решетки. Это, например, изотопы гелия 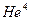 и
и 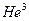 . Для них среднее смещение атома, колеблющегося в режиме нулевых колебаний, равно трем периодам решетки. Такая же ситуация возникает при колебаниях примесных атомов водорода (в связи с малостью его массы) в решетках некоторых тяжелых металлов.
. Для них среднее смещение атома, колеблющегося в режиме нулевых колебаний, равно трем периодам решетки. Такая же ситуация возникает при колебаниях примесных атомов водорода (в связи с малостью его массы) в решетках некоторых тяжелых металлов.
При таких смещениях у атома появляется большая вероятность двигаться по кристаллу с помощью туннельного эффекта, не преодолевая барьер, а проходя под ним. В результате этого квантового эффекта атом или вакансия перестают быть локализованными в узле решетки; такие дефекты А. Ф. Андреев и И. М. Лифшиц назвали дефектонами. Соответственно делокализованные атомы примеси и вакансии - примесоны и вакансоны.
При достаточно низких температурах частота столкновений дефектона с другими дефектонами или фононами мала; и дефектоны являются практически свободно движущимися. С повышением температуры, наступит момент, когда за время, проводимое дефектом на фиксированном узле, он успевает прийти в равновесие с решеткой. Теперь это - локализованный дефект, совершающий случайные (или скоррелированные) блуждания с шагом 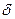 .
.
В низкотемпературной области коэффициент диффузии дефектона определяется известным из молекулярной теории газов выражением 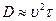 , где
, где 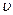 - скорость дефектона, а
- скорость дефектона, а 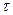 - среднее время между двумя столкновениями дефектона с другими возбуждениями кристалла. Для рассеяния на фононах
- среднее время между двумя столкновениями дефектона с другими возбуждениями кристалла. Для рассеяния на фононах 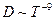 . В металлах основную роль играют столкновения дефектона с электронами. При этом коэффициент диффузии дефектона обратно пропорционален температуре
. В металлах основную роль играют столкновения дефектона с электронами. При этом коэффициент диффузии дефектона обратно пропорционален температуре 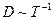 . В обоих случаях коэффициент диффузии не возрастает, а уменьшается с ростом температуры.
. В обоих случаях коэффициент диффузии не возрастает, а уменьшается с ростом температуры.
Как было показано ранее, коэффициент диффузии локализованного дефекта выражается, через частоту его скачков 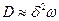 ,
, 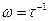 , где
, где 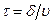 — время, проводимое дефектом на узле решетки. Следовательно, при не слишком высоких температурах
— время, проводимое дефектом на узле решетки. Следовательно, при не слишком высоких температурах 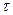 , а, следовательно, и
, а, следовательно, и 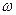 , и коэффициент диффузии не зависят от температуры.
, и коэффициент диффузии не зависят от температуры.
При дальнейшем повышении температуры квантовая задача переходит к классической о дефекте в потенциальной яме, соответствующей положению равновесия; именно той задачей, которая рассматривалась до сих пор.
Таким образом, при понижении температуры коэффициент диффузии дефектов сначала экспоненциально уменьшается (классическая диффузия), выходит на плато (квантовая диффузия локализованных дефектов), а затем возрастает (диффузия дефектонов).
Это относится в равной мере к вакансиям и примесным атомам. При достаточно низких температурах локализованные примеси превращаются в практически свободно движущиеся через кристаллы примесоны. В опытах по диффузии атомов 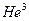 в кристаллах
в кристаллах 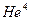 была обнаружена независимость коэффициента диффузии от температуры в области от 1 до 0,4 К (плато), а также предсказанная теорией (для рассеяния примесонов на примесонах) обратная зависимость
была обнаружена независимость коэффициента диффузии от температуры в области от 1 до 0,4 К (плато), а также предсказанная теорией (для рассеяния примесонов на примесонах) обратная зависимость 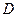 от концентрации
от концентрации 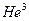 в интервале от 0,75 до 0,92%. Интересно, что коэффициент диффузии измеренный при 1К составил 10-8— 10-9 см2/с, что является очень большой величиной для столь низкой температуры.
в интервале от 0,75 до 0,92%. Интересно, что коэффициент диффузии измеренный при 1К составил 10-8— 10-9 см2/с, что является очень большой величиной для столь низкой температуры.
Дата добавления: 2020-07-18; просмотров: 983;











