Диффузия в твердых растворах замещения
Для большей наглядности и простоты ограничимся анализом двухкомпонентной системы 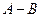 , образующий твёрдый раствор замещения.
, образующий твёрдый раствор замещения.
Если раствор на основе компонента 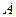 является бесконечно разбавленным, то при диффузии в таком растворе изотопа
является бесконечно разбавленным, то при диффузии в таком растворе изотопа 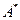 определяется коэффициент изотопной диффузии
определяется коэффициент изотопной диффузии 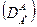 , практически не отличающийся от коэффициента самодиффузии. При диффузии изотопа
, практически не отличающийся от коэффициента самодиффузии. При диффузии изотопа 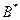 определяется коэффициент изотопной диффузии
определяется коэффициент изотопной диффузии 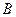 в бесконечно разбавленном растворе на основе
в бесконечно разбавленном растворе на основе 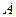 .
.
Если раствор не является бесконечно разбавленным и концентрации компонентов соизмеримы, то и при диффузии изотопа 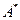 , и при диффузии изотопа
, и при диффузии изотопа 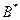 определяются коэффициенты гетеродиффузии
определяются коэффициенты гетеродиффузии 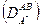 и
и 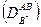 втвёрдом растворе.
втвёрдом растворе.
Можно сформулировать три общих эмпирических правила, описывающих разницу между коэффициентом гетеродиффузии примеси и коэффициентом самодиффузии растворителя в бесконечно разбавленном растворе:
- 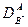 и
и 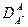 отличаются не более чем на порядок;
отличаются не более чем на порядок;
-предэкспоненциальные факторы также отлича- ются не более чем на порядок;
-энергии активации различаются не более чем на 15%.
Причины этого различия заключаются в следующем. В кристаллах с гцк решеткой коэффициент гетеродиффузии примеси можно записать в виде
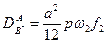 , (2.48)
, (2.48)
где 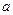 — период решетки;
— период решетки; 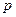 — вероятность обнаружить вакансию среди ближайших соседей атома примеси;
— вероятность обнаружить вакансию среди ближайших соседей атома примеси; 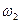 — частота обмена местами между вакансией и атомом примеси;
— частота обмена местами между вакансией и атомом примеси; 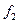 - фактор корреляции, равный в соответствии с уравнением (2.16) и схемой скачка, представленной на рис. 2.6.
- фактор корреляции, равный в соответствии с уравнением (2.16) и схемой скачка, представленной на рис. 2.6.
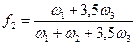 ,
,
где 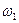 -частота обмена вакансии с атомом растворителя - соседом атома примеси (вакансия была до скачка и остается после скачка соседом атома примеси),
-частота обмена вакансии с атомом растворителя - соседом атома примеси (вакансия была до скачка и остается после скачка соседом атома примеси), 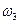 - частота обмена вакансии с атомом растворителя ( в результате вакансия уходит от атома примеси, диссоциативный скачок)
- частота обмена вакансии с атомом растворителя ( в результате вакансия уходит от атома примеси, диссоциативный скачок)
Таким образом, при рассмотрении гетеродиффузии примеси необходимо вводить в рассмотрение как минимум три сорта скачков вакансии, а если учитывать также частоту ассоциативных скачков (см. рис. 2.6), то более точное выражение для 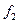 имеет вид
имеет вид
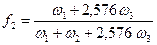 .
.
В гцк решётке чистого растворителя вероятность обнаружить вакансию на 12 местах вокруг произвольного атома 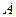
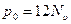 ,
,
где 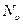 - равновесная атомная доля вакансий, равная
- равновесная атомная доля вакансий, равная 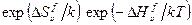 .
.
Вблизи атома примеси эта вероятность изменяется, поскольку между вакансией и атомом примеси существует взаимодействие.
В соответствии со сказанным для комплекса вакансия -атом примеси можно написать, что
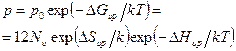 . (2.49)
. (2.49)
Здесь 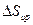 - изменение энтропии, связанное с образованием пары,
- изменение энтропии, связанное с образованием пары, 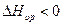 - разница между энтальпией образования вакансии вдали и вблизи от атома примеси. Эта величина, приблизительно совпадает с энергией взаимодействия между вакансией и атомам примеси (
- разница между энтальпией образования вакансии вдали и вблизи от атома примеси. Эта величина, приблизительно совпадает с энергией взаимодействия между вакансией и атомам примеси ( 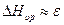 ).
).
Частота скачков вакансии в решётке чистого растворителя
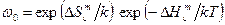 .
.
Естественно предположить, что вблизи атома примеси она изменяется, тогда
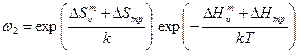 , (2.50)
, (2.50)
где 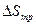 и
и 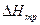 - изменение энтропии и энтальпии перемещения вакансии, когда она обменивается местами не с атомом растворителя, а с атомом примеси.
- изменение энтропии и энтальпии перемещения вакансии, когда она обменивается местами не с атомом растворителя, а с атомом примеси.
Подставляя уравнения (2.49) и (2.50) в (2.48), получим
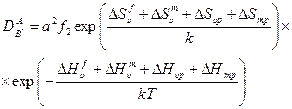 . (2.51)
. (2.51)
Сравним это выражение с коэффициент самодиффузии
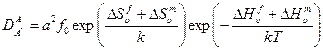 . (2.52)
. (2.52)
Следовательно, изменение предэкспоненциального фактора определяется отношением 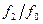 и величинами
и величинами 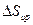 и
и 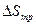 . Естественно предположить, что они малы, поскольку малы
. Естественно предположить, что они малы, поскольку малы 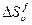 и
и 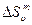 . Отношение
. Отношение 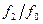 может сильно отличаться от единицы в случае сильной связи между вакансией и атомом примеси. В табл. 2.2 приведены факторы корреляции для гетеродиффузии различных примесей в серебре и отношение
может сильно отличаться от единицы в случае сильной связи между вакансией и атомом примеси. В табл. 2.2 приведены факторы корреляции для гетеродиффузии различных примесей в серебре и отношение 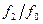 .
.
Изменение энергии активации, как это следует из сравнения уравнений (2.49) и (2.50), составит:
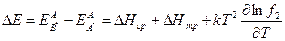 . (2.53)
. (2.53)
| Таблица 2.2 Факторы корреляции для гетеродиффузии примесей в серебре | |||||
| Примесь | 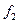
| 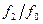
| Примесь | 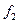
| 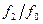
|
| Палладий | 0,96 | 1,23 | Таллий | 0,50 | 0,64 |
| Медь | 0,86 | 1,10 | Германий | 0,39 | 0,50 |
| Кадмий | 0,52 | 0,67 | Свинец | 0,65 | 0,83 |
| Индий | 0,43 | 0,55 | Сурьма | 0,64 | 0,82 |
В случае сильной связи между вакансией и атомом примеси ( 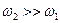 ) коэффициент диффузии
) коэффициент диффузии 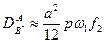 Очевидно, в этом случае энергия активации диффузии есть сумма энергии образования вакансии вблизи атома примеси и энергии перемещения, характерной для чистого растворителя. В величину
Очевидно, в этом случае энергия активации диффузии есть сумма энергии образования вакансии вблизи атома примеси и энергии перемещения, характерной для чистого растворителя. В величину 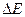 не войдет слагаемое
не войдет слагаемое 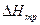 .
.
В случае слабой связи ( 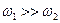 ) фактор
) фактор 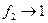 и
и 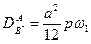 . В энергию активации войдет энергия перемещения, характерная для примесного атома.
. В энергию активации войдет энергия перемещения, характерная для примесного атома.
Теоретическая оценка величин 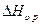 и
и 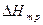 была сделана Дж. Лазарусом для одновалентных растворителей для случая температурной независимости фактора корреляции. Он предположил, что атом примеси вносит в решётку избыточный заряд
была сделана Дж. Лазарусом для одновалентных растворителей для случая температурной независимости фактора корреляции. Он предположил, что атом примеси вносит в решётку избыточный заряд 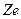 (
( 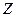 - разница валентностей примеси и одновалентного растворителя). Экранированный потенциал этого заряда можно записать как
- разница валентностей примеси и одновалентного растворителя). Экранированный потенциал этого заряда можно записать как
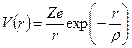 , (2.52)
, (2.52)
где 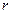 - расстояние от заряда, находящегося в точке
- расстояние от заряда, находящегося в точке 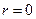 ;
; 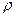 - радиус экранирования, равный
- радиус экранирования, равный 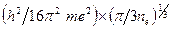 ;
; 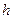 - постоянная Планка;
- постоянная Планка; 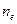 — число электронов в единице объема;
— число электронов в единице объема; 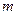 и
и 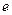 — масса и заряд электрона.
— масса и заряд электрона.
Между вакансией, имеющей заряд -1, и примесным атомом, находящимся на расстоянии 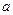 от неё, возникает взаимодействие, и энергия образования вакансии уменьшается на величину
от неё, возникает взаимодействие, и энергия образования вакансии уменьшается на величину
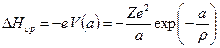 . (2.55)
. (2.55)
Энергия образования вакансии уменьшается, если 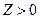 (примесь находится справа от растворителя в периодической системе элементов), и наоборот.
(примесь находится справа от растворителя в периодической системе элементов), и наоборот.
Аналогичным образом Лазарус оценил и 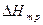 .
.
Эксперимент действительно показывает, что энергия активации гетеродиффузии 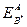 меньше энергии активации самодиффузии
меньше энергии активации самодиффузии 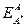 , если
, если 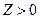 . Теория предсказывает линейную зависимость
. Теория предсказывает линейную зависимость 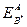 от
от 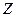 . Это подтверждается опытом для одновалентных растворителей
. Это подтверждается опытом для одновалентных растворителей 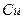 ,
, 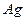 ,
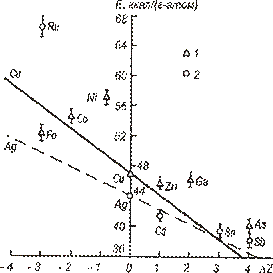
, 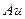 (рис. 2.10).
(рис. 2.10).
|
Рис. 2.10. Зависимость энергии активации ( 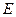 ) диффузии примесей в серебре (1) и меди (2) от разницы валентностей ( ) диффузии примесей в серебре (1) и меди (2) от разницы валентностей ( 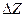 ) )
|
Общее правило, сформулированное Лазарусом, заключается в том, что при добавлении в раствор «быстрой» примеси (т. е. такой, что 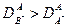 ) оба коэффициента растут, причем коэффициент самодиффузии растворителя (
) оба коэффициента растут, причем коэффициент самодиффузии растворителя ( 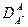 ) растет быстрее, чем гетеродиффузии примеси (
) растет быстрее, чем гетеродиффузии примеси ( 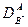 ).Однако это правило не всегда выполняется.
).Однако это правило не всегда выполняется.
Очень часто наблюдают линейную зависимость коэффициента самодиффузии растворителя от концентрации примеси:
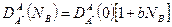 . (2.56)
. (2.56)
Это выражение можно получить теоретически в приближении слабых возмущений, когда малая доля вакансий связана с атомами примеси, пользуясь соответствующим выражением для фактора корреляции. При этом
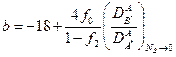 . (2.57)
. (2.57)
Поскольку для металлов с гцк решеткой 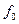 =0,78, можно, измерив
=0,78, можно, измерив 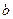 , найти
, найти 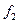 . Существует эмпирическая корреляция между влиянием примеси на самодиффузию растворителя и температуру его плавления:
. Существует эмпирическая корреляция между влиянием примеси на самодиффузию растворителя и температуру его плавления:
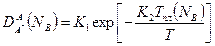 . (2.58)
. (2.58)
где 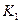 и
и 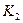 - константы.
- константы.
В итоге на основании вышеприведенных рассуждений следует, что в плотноупакованных решетках (гцк и гпу) преобладает вакансионный механизм диффузии.
В металлах с более открытой решеткой, в частности с оцк решеткой наиболее вероятным представляется вакансионный механизм, однако, нельзя исключить ни прямой межузельный, ни межузельный механизм вытеснения. Некоторые исследователи считают возможным даже обменный механизм.
Наконец, следует упомянуть еще о двух «аномальных» эффектах, имеющих отношение к механизмам диффузии. Для обоих не дано общепринятого теоретического объяснения.
Было обнаружено, что коэффициент диффузии меди в германии очень велик ( 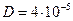 см2/с) и слабо зависит от температуры в интервале 700—900°С. Это видимо связано с тем, что значительная доля атомов примеси находится в междоузлиях. Поскольку коэффициент межузельной диффузии примеси гораздо больше вакансионного, то именно диффузия по междоузлиям определяет экспериментальное значение
см2/с) и слабо зависит от температуры в интервале 700—900°С. Это видимо связано с тем, что значительная доля атомов примеси находится в междоузлиях. Поскольку коэффициент межузельной диффузии примеси гораздо больше вакансионного, то именно диффузия по междоузлиям определяет экспериментальное значение 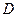 . В дальнейшем такой же эффект был обнаружен для железа в германии и кремнии.
. В дальнейшем такой же эффект был обнаружен для железа в германии и кремнии.
Позднее было показано, что диффузия примесей в элементах с решеткой типа алмаза ( 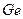 ,
, 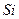 ) - не единственный пример «сверхбыстрой» диффузии в твердом состоянии. Благородные примеси (медь, серебро, золото) диффундируют частично по межузельному механизму в многовалентных растворителях III и IV групп периодической системы, таких как свинец (гцк), олово (тетрагональная), индий (тетрагональная), таллий (гцк). Эффект был обнаружен также для меди в празеодиме как в
) - не единственный пример «сверхбыстрой» диффузии в твердом состоянии. Благородные примеси (медь, серебро, золото) диффундируют частично по межузельному механизму в многовалентных растворителях III и IV групп периодической системы, таких как свинец (гцк), олово (тетрагональная), индий (тетрагональная), таллий (гцк). Эффект был обнаружен также для меди в празеодиме как в 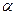 -состоянии (ГПУ), так и
-состоянии (ГПУ), так и 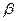 -состоянии (оцк).
-состоянии (оцк).
Коэффициент диффузии примесей, по крайней мере, на три порядка превышает коэффициент самодиффузии, а для меди в олове при 25°С это отношение доходит до 2×109 (в направлении оси 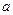 )и 1012 (параллельно оси
)и 1012 (параллельно оси 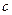 ). Заметим, что радиус атомов золота и серебра составляет около 80% от атомного радиуса свинца и еще большую долю от радиусов олова, индия и таллия, тем не менее, всю совокупность опытных данных удалось объяснить, только приняв предположение о межузельном механизме.
). Заметим, что радиус атомов золота и серебра составляет около 80% от атомного радиуса свинца и еще большую долю от радиусов олова, индия и таллия, тем не менее, всю совокупность опытных данных удалось объяснить, только приняв предположение о межузельном механизме.
Если бы действовал вакансионный механизм, потребовалось бы огромное увеличение частоты скачков иона растворителя в присутствии примеси. Однако добавление к свинцу 0,02% 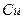 или серебра практически не меняло его подвижности.
или серебра практически не меняло его подвижности.
Было предложено качественное объяснение, почему благородные металлы могут занимать междоузлия в многовалентных растворителях. Обычно этому препятствует сильное ион - ионное отталкивание. Однако ионные радиусы индия, олова, свинца и таллия относительно малы, а междоузлия сравнительно велики, так что перекрытие практически отсутствует. Кроме того, кулоновское отталкивание ионов сильно экранируется большим числом валентных электронов растворителя.
Вместе с тем между 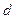 -электронами примеси и растворителя возникает сильное корреляционное взаимодействие. Этому благоприятствует изоэлектронность ионных остовов, а также равенство ион - ионного расстояния с тем, которое есть в примесном металле. Оба условия лучше выполняются для междоузлий и хуже для узлов. Расстояние между последними слишком велико для возникновения эффективной
-электронами примеси и растворителя возникает сильное корреляционное взаимодействие. Этому благоприятствует изоэлектронность ионных остовов, а также равенство ион - ионного расстояния с тем, которое есть в примесном металле. Оба условия лучше выполняются для междоузлий и хуже для узлов. Расстояние между последними слишком велико для возникновения эффективной 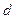 -
- 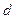 связи.
связи.
Несмотря на непротиворечивость предложенного объяснения, никаких расчетов сделано не было. Стоит отметить, что во всех упомянутых случаях общее содержание примесей не превышало 0,1%. Из теоретического анализа не следует, что это условие является обязательным.
Вторая диффузионная «аномалия» относится к некоторым металлам с оцк решеткой: наиболее ярко она представлена у 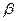 -титана,
-титана, 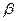 -циркония и
-циркония и 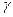 -урана. Для этих металлов в широком интервале над температурой
-урана. Для этих металлов в широком интервале над температурой 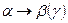 превращения не выполняется линейная зависимость логарифма коэффициента диффузии от обратной температуры. Энергия активации и предэкспоненциальный фактор относительно низки: первая составляет около 60% от
превращения не выполняется линейная зависимость логарифма коэффициента диффузии от обратной температуры. Энергия активации и предэкспоненциальный фактор относительно низки: первая составляет около 60% от 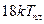 , a
, a 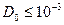 см2/с. Наконец, некоторые примеси диффундируют в них на два порядка быстрее, чем атомы растворителя при самодиффузии (
см2/с. Наконец, некоторые примеси диффундируют в них на два порядка быстрее, чем атомы растворителя при самодиффузии ( 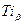 и
и 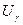 ).
).
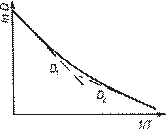
Коэффициент диффузии в этих металлах можно представить в виде суммы двух коэффициентов (рис. 2.11).
|
| Рис.2.11. Зависимость коэффициента диффузии от температуры в аномальных металлах с оцк решёткой |
Первый высокотемпературный коэффициент 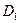 подчиняется правилам вакансионной диффузии и характеризует свойства данного металла; это истинный коэффициент диффузии. Второй, низкотемпературный коэффициент
подчиняется правилам вакансионной диффузии и характеризует свойства данного металла; это истинный коэффициент диффузии. Второй, низкотемпературный коэффициент 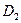 , очень чувствительный к условиям проведения диффузионного опыта. Можно отметить, что все эти металлы претерпевают при нагреве фазовый переход
, очень чувствительный к условиям проведения диффузионного опыта. Можно отметить, что все эти металлы претерпевают при нагреве фазовый переход 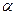 (г.п.у.) -
(г.п.у.) - 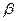 (оцк). Поэтому получила широкое распространение точка зрения, что
(оцк). Поэтому получила широкое распространение точка зрения, что 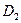 соответствует диффузии по дефектам, например дислокациям, возникающим при полиморфном превращении.
соответствует диффузии по дефектам, например дислокациям, возникающим при полиморфном превращении.
Другое объяснение основано на предположении, что в низкотемпературной области аномальные металлы содержат много примесных вакансий, сильно связанных с кислородом, от которого оцк металлы очень трудно очистить. Поскольку эти вакансии не являются термически равновесными, то энергия активации диффузии определяется не суммой энергий образования и перемещения вакансий, а одной энергией перемещения. Эта модель требует большой энергии связи между атомом кислорода и вакансией, не менее 0,5 эВ. Для нормальных металлов это невозможно, так как электроны проводимости эффективно экранируют возмущающий потенциал атома примеси. Однако в металлах с незаполненной 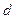 -оболочкой исключить полностью такую возможность нельзя. Это показывает, что электронные эффекты могут, по-видимому, играть существенную роль в диффузии особенно для переходных металлов.
-оболочкой исключить полностью такую возможность нельзя. Это показывает, что электронные эффекты могут, по-видимому, играть существенную роль в диффузии особенно для переходных металлов.
Наконец, третье объяснение предполагает возникновение в этих металлах вблизи точки фазового перехода особого предпереходного состояния, связанного с динамическими кооперативными смещениями атомов.
Дата добавления: 2020-07-18; просмотров: 913;











