Анализ диффузии по границам зерен
О роли диффузии по границам зерен, например, можно судить по рис. 3.1.
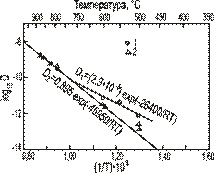
На нем показан коэффициент самодиффузии серебра в моно- и поликристалле. Коэффициент диффузии определяли следующим образом. На поверхность серебряного образца наносили радиоактивное серебро и после диффузионного отжига находили коэффициент  по наклону прямой в координатах «логарифм активности - квадрат глубины проникновения».
по наклону прямой в координатах «логарифм активности - квадрат глубины проникновения».
|
| Рис. 3.1. Значения коэффициента самодиффузии серебра в монокристалле (2) и поликристалле (1) |
При высоких температурах значения коэффициента  одни и те же для обоих образцов. Однако ниже 700°С значение
одни и те же для обоих образцов. Однако ниже 700°С значение  поликристалла больше, чем для монокристалла. Путями ускоренной диффузии в этом случае являются границы зерен. Видно, что вклад диффузии по границам зерен заметен около 600°С и преобладает при более низких температурах.
поликристалла больше, чем для монокристалла. Путями ускоренной диффузии в этом случае являются границы зерен. Видно, что вклад диффузии по границам зерен заметен около 600°С и преобладает при более низких температурах.
Для чистого поликристаллического серебра с размером зерна порядка 1мм ишириной границы равной 3×10-8см примерно один атом из миллиона сидит на границе. При 700°С границы зерен удваивают измеряемую величину коэффициента диффузии. Если одна миллионная часть атомов создает поток, сравнимый с потоком, создаваемым всеми остальными, то каждый из атомов на границе должен, грубо говоря, перескакивать в миллион раз чаще, чем атомы регулярной решетки. При низких температурах эта разница должна быть еще больше. Так как атомов на границах зерен очень мало по сравнению с решеткой, то даже если средняя частота перескоков на границе будет на несколько порядков больше, чем в решетке, то границы все же не дадут заметной добавки в суммарный поток.
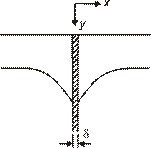
Для определения значения коэффициента диффузии по границам зерен ( 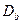 ) из диффузионных опытов с бикристаллами Фишер предложил рассматривать границу как тонкий слой материала с высоким коэффициентом диффузии, лежащий между двумя зернами, имеющими низкий коэффициент диффузии. На рис. 3.2 показано сечение, перпендикулярное границе, и внешняя поверхность. На последнюю (плоскость
) из диффузионных опытов с бикристаллами Фишер предложил рассматривать границу как тонкий слой материала с высоким коэффициентом диффузии, лежащий между двумя зернами, имеющими низкий коэффициент диффузии. На рис. 3.2 показано сечение, перпендикулярное границе, и внешняя поверхность. На последнюю (плоскость 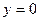 ) нанесен слой радиоактивного вещества, которое диффундирует вглубь образца.
) нанесен слой радиоактивного вещества, которое диффундирует вглубь образца.
| 
|
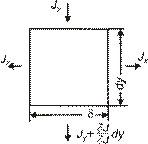
| Рис. 3.2. Координатные оси и изоконцентрационный контур - сечение модели, используемой для описания пограничной диффузии | Рис. 3.3. Потоки, направленные внутрь и из элемента граничного слоя |
Для определения 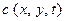 можно ввести граничные условия:
можно ввести граничные условия:
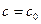 при
при 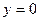 и
и 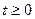 ;
; 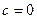 при
при 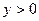 и
и 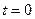 .
.
Предполагается, что поперек границы нет градиента концентрации, а при переходе от границы зерна к зерну концентрация меняется непрерывно.
Чтобы получить дифференциальное уравнение, описывающее диффузию в граничном слое, рассмотрим элемент этого слоя единичной глубины, длинной 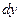 ишириной
ишириной 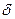 . Потоки через грани этого элемента, перпендикулярные осям
. Потоки через грани этого элемента, перпендикулярные осям 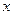 и
и 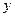 , показаны на рис. 3.3. Любая плоскость, перпендикулярная оси
, показаны на рис. 3.3. Любая плоскость, перпендикулярная оси 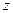 , является плоскостью симметрии, поэтому величина
, является плоскостью симметрии, поэтому величина 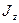 должна быть равна нулю. Изменение концентрации со временем (
должна быть равна нулю. Изменение концентрации со временем ( 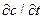 ) можно записать как
) можно записать как
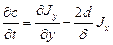 (3.1)
(3.1)
где 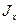 - поток из границы в объем равный
- поток из границы в объем равный 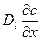 , причем здесь градиент берётся в объеме, в точке стыка с граничным слоем. Если
, причем здесь градиент берётся в объеме, в точке стыка с граничным слоем. Если 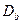 - коэффициент диффузии по границе зерна, то
- коэффициент диффузии по границе зерна, то
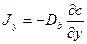 . (3.2)
. (3.2)
Подставляя выражение (3.2) в (3.1), получим
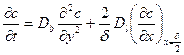 . (3.3)
. (3.3)
Вне границы диффузия описывается вторым уравнением Фика:
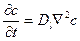 . (3.4)
. (3.4)
Таким образом, задача сводится к тому, чтобы найти решение, непрерывное при переходе через поверхность раздела между границей и зерном 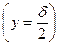 и удовлетворяющее обоим уравнениям в соответствующих районах.
и удовлетворяющее обоим уравнениям в соответствующих районах.
Анализируя численные решения уравнений (3.3) и (3.4), Фишер пришел к выводу, что концентрация на границе вначале растет быстро, но затем скорость роста падает. Поэтому после длительного отжига концентрация в любой точке границы 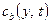 близка к конечному значению. Чтобы упростить решение, он предположил, что граничная концентрация устанавливается, практически мгновенно и на любом расстоянии от поверхности образца остается постоянной в любой момент времени. Кроме того, поток растворенного вещества, уходящего с границы в зерно, перпендикулярен границе. Это позволяет заменить исходную модель набором пластин толщиной
близка к конечному значению. Чтобы упростить решение, он предположил, что граничная концентрация устанавливается, практически мгновенно и на любом расстоянии от поверхности образца остается постоянной в любой момент времени. Кроме того, поток растворенного вещества, уходящего с границы в зерно, перпендикулярен границе. Это позволяет заменить исходную модель набором пластин толщиной 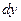 , перпендикулярных оси
, перпендикулярных оси 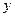 . Все они разделены непроницаемыми мембранами (так что весь объемный поток направлен по нормали к граничному слою). В момент
. Все они разделены непроницаемыми мембранами (так что весь объемный поток направлен по нормали к граничному слою). В момент 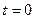 в каждой пластине, в граничном слое устанавливается некоторая постоянная концентрация
в каждой пластине, в граничном слое устанавливается некоторая постоянная концентрация 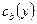 . Тогда концентрацию в любой точке пластины можно записать как
. Тогда концентрацию в любой точке пластины можно записать как
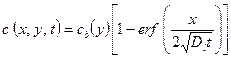 . (3.5)
. (3.5)
Соединив точки равной концентрации в «пластинчатой» модели, получим изоконцентрационные контуры в реальном образце. В этом случае
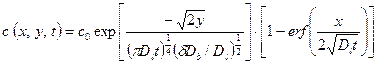 . (3.6)
. (3.6)
Экспериментально проще всего найти количество радиоактивного вещества в каждой пластине толщиной 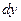 , параллельной свободной поверхности. Эта величина равна количеству растворенного вещества, «отсосанного» пластиной из границы
, параллельной свободной поверхности. Эта величина равна количеству растворенного вещества, «отсосанного» пластиной из границы
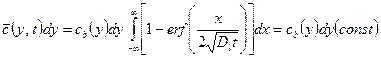 . (3.7)
. (3.7)
Графическая зависимость в координатах 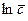 -
- 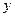 представляет прямую, наклон которой равен
представляет прямую, наклон которой равен
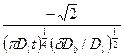 . (3.8)
. (3.8)
Это решение справедливо только для глубин 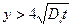 , куда большая часть радиоактивного вещества доходит благодаря диффузии по границе зерна, а не по матрице параллельно границе. Из эксперимента следует, что это возможно, если
, куда большая часть радиоактивного вещества доходит благодаря диффузии по границе зерна, а не по матрице параллельно границе. Из эксперимента следует, что это возможно, если 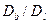 достаточно велико. Но в анализе Фишера нет критерия, позволяющего уточнить, что значит «достаточно велико».
достаточно велико. Но в анализе Фишера нет критерия, позволяющего уточнить, что значит «достаточно велико».
| 
|
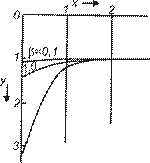
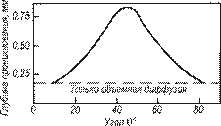
Рис. 3.4. Концентрационные контуры для 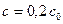 . Показано избыточное проникновение вещества по границе для различных значений . Показано избыточное проникновение вещества по границе для различных значений 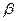 . Единица по оси ординат отвечает глубине проникновения в отсутствие границы . Единица по оси ординат отвечает глубине проникновения в отсутствие границы
|
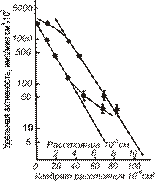
Рис. 3.5. Влияние границ (зерен 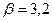 ). Диффузия изотопа цинка в поликристаллическом цинке (отжиг при 151°С в течение 312,5 ч) ). Диффузия изотопа цинка в поликристаллическом цинке (отжиг при 151°С в течение 312,5 ч)
|
В работе Уиппла были получены концентрационные контуры для 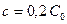 и
и 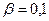 ; 1,0 и 10, где
; 1,0 и 10, где 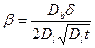 (рис. 3.4). Очевидно, что, пока
(рис. 3.4). Очевидно, что, пока 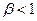 , заметного проникновения вдоль границ, опережающего проникновение по зерну нет. Это значит, что при
, заметного проникновения вдоль границ, опережающего проникновение по зерну нет. Это значит, что при 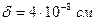 ;
; 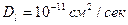 и
и 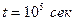 величина
величина 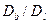 должна быть больше чем 5×104. Физический смысл в том, что граничный слой слишком тонок и поток по нему слишком мал, чтобы повлиять на распределение концентрации, пока не будет
должна быть больше чем 5×104. Физический смысл в том, что граничный слой слишком тонок и поток по нему слишком мал, чтобы повлиять на распределение концентрации, пока не будет 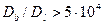 .
.
Влияние границ зерен на значение 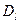 , показана Вайдом на поликристаллическом цинке. Плоский торец цилиндрических образцов покрывали радиоактивным цинком. Затем образцы отжигали и снимали слои, параллельные нанесенному слою. Диффузия изучена в температурном интервале, где преобладает проникновение по границам (
, показана Вайдом на поликристаллическом цинке. Плоский торец цилиндрических образцов покрывали радиоактивным цинком. Затем образцы отжигали и снимали слои, параллельные нанесенному слою. Диффузия изучена в температурном интервале, где преобладает проникновение по границам ( 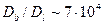 и
и 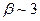 ). Кривая зависимости активности (концентрации) от расстояния приведена на рис. 3.5. Анализируя полученные данные можно сделать следующие выводы:
). Кривая зависимости активности (концентрации) от расстояния приведена на рис. 3.5. Анализируя полученные данные можно сделать следующие выводы:
1. Экспериментальные точки не отклоняются от прямой в координатах 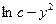 до
до 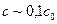 . Это не противоречит результатам Уиппла, который показал, что для фиксированного
. Это не противоречит результатам Уиппла, который показал, что для фиксированного 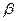 концентрационные контуры (типа приведенных на рис. 3.4) становятся более заостренными к границе по мере уменьшения величины концентрации.
концентрационные контуры (типа приведенных на рис. 3.4) становятся более заостренными к границе по мере уменьшения величины концентрации.
2. Вычисленная величина 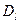 в 6,5 раза больше истинного значения, полученного экстраполяцией от высоких температур, хотя точки ложатся на прямую
в 6,5 раза больше истинного значения, полученного экстраполяцией от высоких температур, хотя точки ложатся на прямую 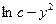 . Поэтому линейная зависимость
. Поэтому линейная зависимость 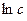 от
от 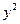 - очень плохое доказательство отсутствия пограничной диффузии.
- очень плохое доказательство отсутствия пограничной диффузии.
3. При совсем «низких» температурах, например при 90°С для цинка, все точки ложатся на прямую 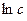 -
- 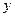 . В этом интервале
. В этом интервале 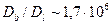 . Если рассчитать
. Если рассчитать 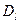 экстраполяцией от высоких температур, то значение
экстраполяцией от высоких температур, то значение 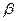 составляет около 103.
составляет около 103.
Следует подчеркнуть, что, несмотря на отличие физических моделей, примерно те же математические вычисления и формулы можно применять для описания поверхностной диффузии. Слой на рис. 3.1 расположен в плоскости симметрии, так что суммарный поток через него, равен нулю. Поэтому если, оставив слой, характеризующийся высокой скоростью диффузии, удалить левую от этого слоя половину бикристалла, то он будет соответствовать поверхности раздела твердого тела с его паром. Единственное, что надо изменить в выражении (3.3), - это убрать двойку, так как из показанного на рис. 3.2 элемента объема материал в объем уходит теперь только с одной стороны.
Существует большое множество моделей границ зёрен. Для малоугловых границ (границы с малым углом разориентировки), общепринятой является дислокационная модель. Однако даже для этой модели нет количественной теории, позволяющей найти отношение 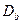 к
к 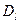 . К основным достижениям в этой области следует отнести несколько систематических исследований по определению влияния температуры и структуры границ на пограничную диффузию (табл. 3.1).
. К основным достижениям в этой области следует отнести несколько систематических исследований по определению влияния температуры и структуры границ на пограничную диффузию (табл. 3.1).
| Таблица 3.1 Значения и для пограничной и объемной диффузии | ||||
| Элемент | 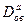 , см2/сек , см2/сек
| 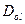 , см2/сек , см2/сек
| 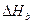 кдж/моль
ккал/моль
кдж/моль
ккал/моль
| 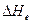 кдж/моль
ккал/моль
кдж/моль
ккал/моль
|
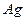
| 0,09 | 0,7 | 90,0 (21,5) | 188 (45) |
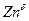
| 0,14 | 0,4 | 58,6 (14) | 96,3 (23) |
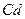
| 0,7 | 0,1 | 54,5 (13) | 77,4 (18,5) |
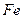
| 8,8в | 167 (40) | 268 (64) |
Из рис. 3.1 видно, что граничные эффекты в поликристаллическом серебре можно измерить только при температуре ниже 750°С и по мере понижения температуры их относительная роль возрастает. Этот вывод имеет общий характер, справедливый для всех изученных металлов и свидетельствует, что энергия активации пограничной диффузии существенно меньше, чем объемной. Некоторые значения 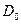 и
и  для пограничной и объемной диффузии приведены в табл. 3.1.
для пограничной и объемной диффузии приведены в табл. 3.1.
В дислокационной модели граница должна иметь много относительно пустых (открытых) участков. В них энергия образования вакансии или перемещения атома в вакансию значительно меньше, чем в объеме. Поэтому видимо энергия активации самодиффузии по границе меньше, чем в объеме.
| 
|
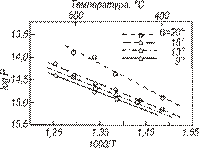
| Рис. 3.6. Проникновение серебра вдоль (100) наклонных границ в меди после отжига в течение двух недель при 675ºС | Рис. 3.7. Зависимость 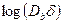 серебра от температуры для различных серебра от температуры для различных 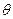 в (100) наклонных границ в (100) наклонных границ
|
Первое систематическое исследование изменения 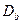 с разориентировкой зёрен было выполнено Смолуховским и др. Они наносили радиоактивное серебро на поверхность медного образца, состоявшего из столбчатых зерен, ориентированных по нормали к поверхности. После диффузионного отжига снимали слои параллельно поверхности до тех пор, пока детектор не переставал регистрировать наличие радиоактивного серебра в зернах. Эту глубину проникновения фиксировали, после чего слои снимали дальше, пока уже авторадиография не обнаруживала растворенного серебра на границе. Характерные результаты показаны на рис. 3.6 для симметричных наклонных границ. Здесь
с разориентировкой зёрен было выполнено Смолуховским и др. Они наносили радиоактивное серебро на поверхность медного образца, состоявшего из столбчатых зерен, ориентированных по нормали к поверхности. После диффузионного отжига снимали слои параллельно поверхности до тех пор, пока детектор не переставал регистрировать наличие радиоактивного серебра в зернах. Эту глубину проникновения фиксировали, после чего слои снимали дальше, пока уже авторадиография не обнаруживала растворенного серебра на границе. Характерные результаты показаны на рис. 3.6 для симметричных наклонных границ. Здесь 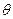 - угол, на который надо повернуть кристаллы вокруг оси [100] друг относительно друга, чтобы совместить их. Преимущественного проникновения по границам не наблюдается, если угол
- угол, на который надо повернуть кристаллы вокруг оси [100] друг относительно друга, чтобы совместить их. Преимущественного проникновения по границам не наблюдается, если угол 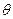 =10° или больше 80°, ,но при
=10° или больше 80°, ,но при 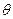 >10° оно растет, достигает максимума при
>10° оно растет, достигает максимума при 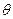 = 45°, а затем опять падает до нуля при
= 45°, а затем опять падает до нуля при 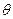 ≈80°. Аналогичные эффекты наблюдались для других металлов и наклонных границ другого типа.
≈80°. Аналогичные эффекты наблюдались для других металлов и наклонных границ другого типа.
Гофман и Тарнбал количественно измерили отношение 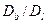 в серебре для симметричных наклонных границ в интервале 9°≤
в серебре для симметричных наклонных границ в интервале 9°≤ 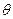 ≤28°. (рис. 3.7), где
≤28°. (рис. 3.7), где 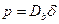 . Величина
. Величина  остается постоянной для углов разориентировки 9, 13 и 16°, но
остается постоянной для углов разориентировки 9, 13 и 16°, но 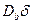 растет с увеличением угла
растет с увеличением угла 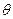 .
.
В соответствие с дислокационной моделью малоугловая граница наклона состоит из ряда линейных параллельных дислокаций отстоящих друг от друга на 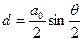 . Решётка между ядрами дислокаций упруго деформирована, но не искажена. Тарнбал и Гофман предполагали, что внутри дислокаций коэффициент диффузии гораздо больше
. Решётка между ядрами дислокаций упруго деформирована, но не искажена. Тарнбал и Гофман предполагали, что внутри дислокаций коэффициент диффузии гораздо больше 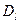 . Поэтому они моделировали границу не в виде слоя с толщиной
. Поэтому они моделировали границу не в виде слоя с толщиной 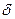 и коэффициентом диффузии
и коэффициентом диффузии 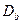 , а в виде плоского ряда «дислокационных трубок» с сечением
, а в виде плоского ряда «дислокационных трубок» с сечением 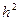 и расстоянием
и расстоянием 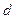 . Для диффузии в направлении этих трубок можно написать
. Для диффузии в направлении этих трубок можно написать
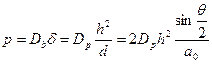 . (3.9)
. (3.9)
Если предположить, что 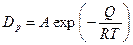 , то в пределах применимости модели трубок
, то в пределах применимости модели трубок 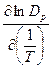 не зависит от
не зависит от 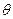 , а
, а 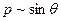 при заданной температуре. И то и другое подтверждается результатами для границ с углом разориентировки 9, 13 и 16°. Принимая
при заданной температуре. И то и другое подтверждается результатами для границ с углом разориентировки 9, 13 и 16°. Принимая 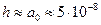 см, получим
см, получим
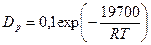 см2/сек. (3.10)
см2/сек. (3.10)
Отсюда следует, что отсутствие преимущественной диффузии по границам при 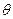 ≤ 10° (рис. 3.6) есть результат недостаточного разрешения метода и высокой температуры отжига.
≤ 10° (рис. 3.6) есть результат недостаточного разрешения метода и высокой температуры отжига.
Из модели трубок следует, что в малоугловых границах избыточная диффузия в направлении, параллельном трубкам 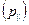 , должна быть больше, чем в перпендикулярном
, должна быть больше, чем в перпендикулярном 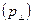 . Эта анизотропия, т. е.
. Эта анизотропия, т. е. 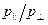 >>1, должна становиться отчетливее при уменьшении угла
>>1, должна становиться отчетливее при уменьшении угла 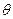 . Для больших значений
. Для больших значений 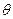 , когда дислокационная модель не пригодна, можно ожидать изотропии.
, когда дислокационная модель не пригодна, можно ожидать изотропии.
|
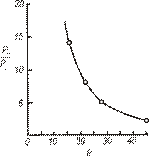
Рис. 3.8. Зависимость анизотропии диффузии в серебре по (100) наклонным границам от 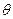 (T =450ºС) (T =450ºС)
|
На рис. 3.8. представлены результаты Гофмана для симметричных наклонных границ в серебре. Анизотропия действительно уменьшается с ростом значения 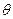 , однако она остается и при высоких
, однако она остается и при высоких 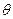 , когда дислокационная модель уже не применима, вплоть до
, когда дислокационная модель уже не применима, вплоть до 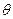 = 45°. Поэтому предположение, что большеугловые границы представляют собой однородный, изотропный слой, очевидно, не верно, и к нему следует относиться весьма осторожно.
= 45°. Поэтому предположение, что большеугловые границы представляют собой однородный, изотропный слой, очевидно, не верно, и к нему следует относиться весьма осторожно.
Влияние дислокаций
В хорошо отожженном монокристалле любая плоскость перерезает 106-107 дислокаций на квадратный сантиметр. Если бы плоскость проходила перпендикулярно границе в бикристаллах с наклонными границами и углами разориентировки 9, 13 и 16°, то она перерезала бы 107 дислокаций на квадратный сантиметр поверхности сечения. Основное различие между этими двумя случаями заключается в том, что во втором - все линии дислокаций параллельны, а в первом — дислокации располагаются во всех направлениях. Поэтому граница зерна увеличивает скорость диффузии в направлении границы, а случайно ориентированные дислокации в монокристалле - по всем направлениям. Аналогом пограничной диффузии в теплопроводности является полоска алюминиевой фольги между двумя кусками пластика. Аналогом же отожженного монокристалла был бы пластик, в котором случайным образом разбросаны алюминиевые проволочки.
Выразим измеренный на опыте или макроскопический коэффициент диффузии 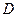 через коэффициенты объёмной и дислокационной диффузии
через коэффициенты объёмной и дислокационной диффузии 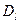 и
и 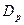 соответственно. Для этого используем подход, принятый в теории случайных блужданий. Ранее было показано, что если каждый атом делает
соответственно. Для этого используем подход, принятый в теории случайных блужданий. Ранее было показано, что если каждый атом делает 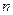 прыжков то суммарное смещение равно
прыжков то суммарное смещение равно 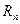 . Пренебрегая эффектами корреляции и предполагая, что длина любого перескока равна
. Пренебрегая эффектами корреляции и предполагая, что длина любого перескока равна 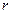 , можно записать
, можно записать
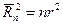 .(3.11)
.(3.11)
Пусть из 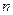 прыжков атом
прыжков атом 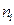 совершил в неискаженной решетке, а
совершил в неискаженной решетке, а 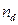 - в дислокационной трубке. Усредняя по многим атомам, получим
- в дислокационной трубке. Усредняя по многим атомам, получим
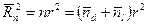 .(3.12)
.(3.12)
Частоты перескоков внутри дислокаций и вне равны
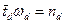 ;
; 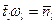 ,
,
где 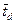 и
и 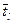 - среднее время пребывания атома в участках с высоким коэффициентом диффузии вокруг ядра дислокации и вне их. Подставляя эти выражения в формулу (3.12) и поделив на среднее время, за которое атом делает
- среднее время пребывания атома в участках с высоким коэффициентом диффузии вокруг ядра дислокации и вне их. Подставляя эти выражения в формулу (3.12) и поделив на среднее время, за которое атом делает 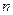 прыжков, получим:
прыжков, получим:
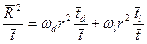 .
.
Отношение 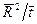 , с точностью до геометрических постоянных, равно макроскопическому коэффициенту диффузии
, с точностью до геометрических постоянных, равно макроскопическому коэффициенту диффузии 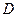 , а
, а 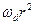 и
и 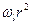 равны
равны 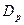 и
и 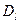 соответственно. Поэтому для монокристалла
соответственно. Поэтому для монокристалла
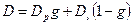 ,(3.13)
,(3.13)
где 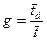 .
.
При самодиффузии в чистом металле все атомы эквивалентны и доля времени, которое меченый атом проводит «внутри» дислокации, равна доле мест, там расположенных. Принимая плотность дислокаций 107 см-2 и число атомов «внутри» каждой дислокации равным 10, имеем
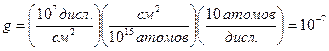 .
.
Так как 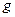 очень мало, можно переписать уравнение (3.13):
очень мало, можно переписать уравнение (3.13):
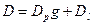
или
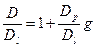 . (3. 14)
. (3. 14)
Используя выражение (3.10) для 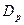 в серебре (табл. 5), получим
в серебре (табл. 5), получим
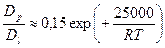 . (3.15)
. (3.15)
При 500° С по этой формуле 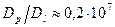 ; подставляя это значение в выражение (3.14), получим
; подставляя это значение в выражение (3.14), получим 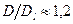 .
.
Чтобы подчеркнуть важность дислокационного вклада при низких температурах, рассмотрим данные, приведенные в табл. 3.2.
Таблица 3.2
Значения 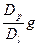 для серебра при различных температурах для серебра при различных температурах 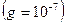
| ||
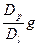
| 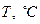
| 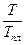
|
| 0,08 | 0,7 | |
| 0,90 | 0,6 | |
| 0,5 | ||
| 0,4 |
Данная таблица сделана для серебра, однако, отношение 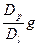 будет примерно таким же и для других металлов. При температурах порядка или меньше половины температуры плавления суммарный коэффициент диффузии образца целиком определяется плотностью дислокаций и значения
будет примерно таким же и для других металлов. При температурах порядка или меньше половины температуры плавления суммарный коэффициент диффузии образца целиком определяется плотностью дислокаций и значения 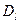 , экстраполированные от высоких температур, почти или совсем не имеют отношения к скорости переноса вещества.
, экстраполированные от высоких температур, почти или совсем не имеют отношения к скорости переноса вещества.
Вопрос о влиянии дислокаций на диффузию в чистых металлах имеет несколько важных аспектов. Это влияние устанавливает определенные пределы температурного интервала, в котором можно точно определить значение  самодиффузии с помощью меченых атомов. Чем точнее необходимо определить значение
самодиффузии с помощью меченых атомов. Чем точнее необходимо определить значение 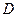 , тем меньше должен быть вклад дислокационных трубок. Единственное, что можно предпринять для уменьшения влияния дислокаций (при заданной их плотности), - это повысить температуру.
, тем меньше должен быть вклад дислокационных трубок. Единственное, что можно предпринять для уменьшения влияния дислокаций (при заданной их плотности), - это повысить температуру.
Аналогичная трудность возникает при попытках точного измерения  граничной диффузии. Уже было показано, что вклад границ достаточен для точного определения
граничной диффузии. Уже было показано, что вклад границ достаточен для точного определения 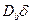 , только если
, только если 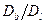 порядка 105 или больше. Грубо говоря, это значит, что температура опыта должна быть меньше
порядка 105 или больше. Грубо говоря, это значит, что температура опыта должна быть меньше 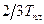 . Однако, если
. Однако, если 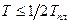 , то влияние дислокаций на
, то влияние дислокаций на 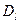 настолько велико, что уже нельзя найти
настолько велико, что уже нельзя найти 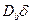 из определяемой на опыте величины
из определяемой на опыте величины 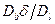 . Таким образом, интервал температур, в котором можно измерять
. Таким образом, интервал температур, в котором можно измерять 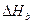 , относительно мал и значения
, относительно мал и значения  не слишком точны.
не слишком точны.
Разница между перемещением растворителя и растворенного вещества вблизи дислокаций не вполне ясна. Однако частично она является результатом возможного взаимодействия дислокаций и растворенных атомов. Если это притяжение, - то доля времени, которое атомы проводят «внутри» дислокации, больше, чем доля мест в ней. Мортлок предположил, что эта доля 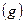 может быть приближенно выражена как
может быть приближенно выражена как 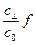 , где
, где 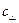 - равновесная концентрация атомов «внутри» дислокации,
- равновесная концентрация атомов «внутри» дислокации, 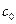 - концентрация растворенного вещества в правильной решетке и
- концентрация растворенного вещества в правильной решетке и 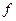 - доля мест «внутри» дислокаций. Тогда отношение определяемого коэффициента диффузии растворенного вещества к истинному можно записать в виде:
- доля мест «внутри» дислокаций. Тогда отношение определяемого коэффициента диффузии растворенного вещества к истинному можно записать в виде:
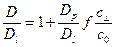 . (3.16)
. (3.16)
Влияние взаимодействия может быть заметным. Например, в случае железа и кобальта в меди Мортлок пришел к выводу, что 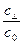 заключено между 10 и 100.
заключено между 10 и 100.
Дата добавления: 2020-07-18; просмотров: 1136;











