Основы теории подобия

Основные трудности дальнейшего анализа конвективного теплообмена связаны с установлением вида зависимости коэффициента теплоотдачи от определяющих его параметров. В большинстве случаев вид этих зависимостей устанавливается при обобщении экспериментальных данных.

Изложим основные принципы, на которых основаны методы обобщения данных эксперимента по изучению конвективного теплообмена. Предположим, что экспериментально в условиях свободной конвекцииудалось измерить коэффициент теплоотдачи проволок разного диаметра d в различных средах при разных значениях температурных напоров (t—t_с). Свойства среды, как показывает более детальный анализ, для явления свободной конвекции описываются следующими параметрами:

коэффициентом термического расширения среды β;

теплопроводностью λ;

теплоемкостью c_p;

плотностью ρ;

динамическим коэффициентом вязкости μ или ν = μ/ρ.

Помимо этих параметров необходимо учитывать ускорение силы тяжести g.Следовательно,

α =f(t, t_с, β, λ, c_p, μ, ρ, g, d). (3)

Получение такого рода экспериментальных зависимостей является практически нереальной задачей из-за большого числа параметров, от которых зависит изучаемый процесс. Однако одиночные эксперименты можно обобщить на большое число случаев на основе теории подобия. В этой теории показано, что протекание сложных физических процессов характеризуется не отдельными физическими и геометрическими величинами, а числами подобия — безразмерными степенными комплексами, составленными из величин, существенных для данного процесса. Например, на теплообмен при свободной конвекции существенно влияет около десятка физических величин. Если на основе теории подобия объединить физические и геометрические параметры в безразмерные комплексы, тот же процесс можно описать не десятью, а следующими тремя комплексами: числом Нуссельта Nu, числом Грасгофа Gr, числом Прандтля Рг:

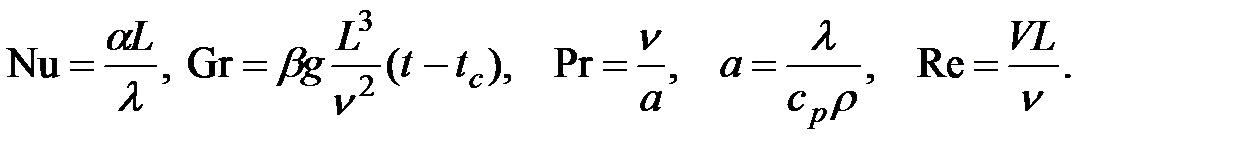(4)

(Для вынужденной конвекции добавляют критерий Рейнольдса Re).

В формулах (4) через L обозначен геометрический размер, характерный для тела данной конфигурации (диаметр для труб или шаров, высота плиты и т. д.). Итак, зависимость (4) можно представить в виде безразмерного уравнения, связывающего три числа подобия,

Nu = F(Gr, Рr), (5)

которое называют уравнением подобия или критериальным уравнением.