Методы теплового моделирования конструкции ЭС

Наиболее часто тепловое моделирование выполняется методами изотермических поверхностей, однородного анизотропного тела и экспериментальными методами.

Метод изотермических поверхностей основан на выделении в конструкции поверхностей с одинаковыми или условно одинаковыми температурами в каждой точке поверхности. Считается, что теплообмен осуществляется между этими поверхностями. В зависимости от конкретной задачи исследования к изотермическим поверхностям конструкций относят поверхность корпуса со среднеповерхностной температурой t _к , поверхность нагретой зоны с температурой t _з , поверхность отдельной функциональной ячейки с температурой t _зi, поверхность отдельного радиоэлемента с температурой t_э и т.д.

Пример построения тепловой модели конструкции блока разъемного типа методом изотермических поверхностей приведен на рис. 1.

Как следует из рис. 1,а, среднеповерхностные температуры представляют собой среднеарифметические значения реальных температур различных точках поверхности, т.е.

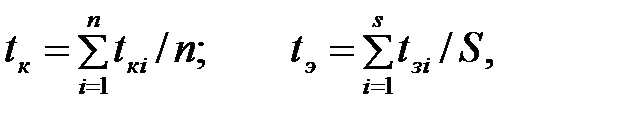и т.д

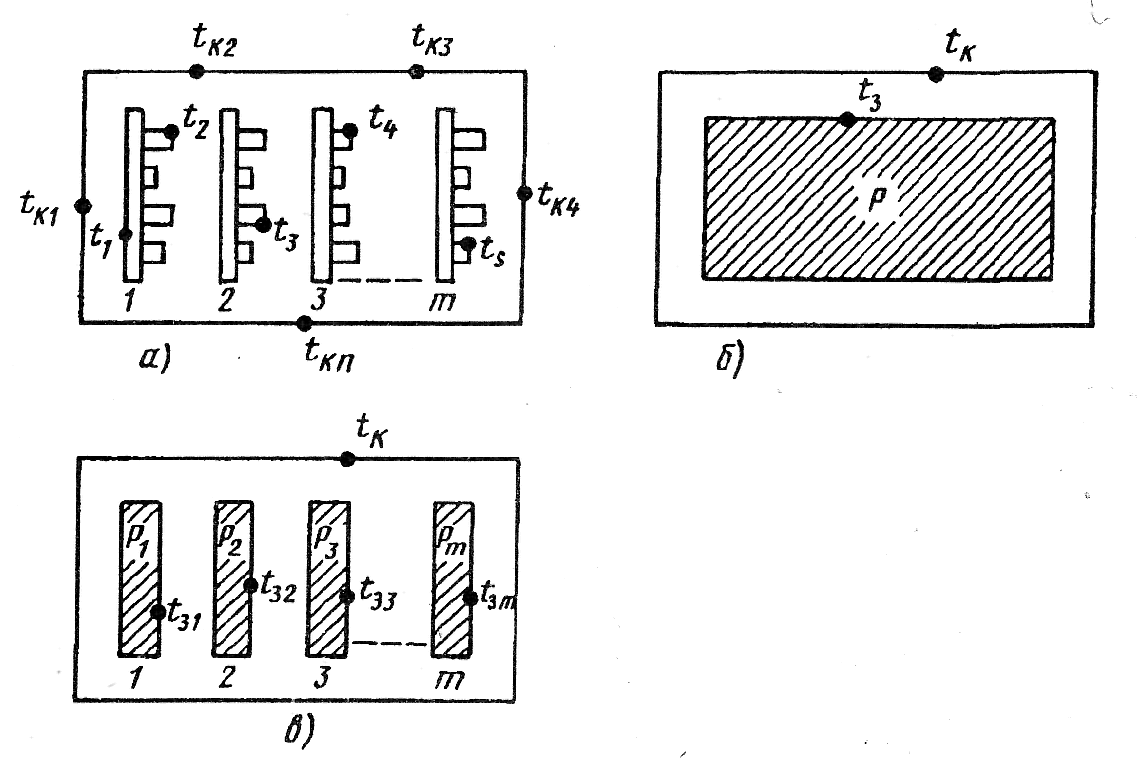
Рис. 1. Построение тепловой модели блока методом изотермических поверхностей а — схематическое изображение конструкции; б — модель для определения средней поверхностной температуры нагретой зоны; в —модель для определения среднеповерхностных температур функциональных ячеек

Таким образом, метод изотермических поверхностей позволяет находить лишь среднеповерхностные температуры. Детализация тепловой модели дает возможность довести решение до определения температуры отдельного радиоэлемента, однако при этом резко возрасте сложность задачи.

Метод однородного анизотропного тела состоит в представлении реальной конструкции или ее части однородным анизотропным телом в виде прямоугольного параллелепипеда с внутренними источниками тепла, для которого находят эквивалентные коэффициенты теплопроводности λ_x , λ_y и λ_z по направлениям осей координат, перпендикулярных граням параллелепипеда. При известных коэффициента теплопроводности и геометрических размерах l_x , l_y , l_z однородного анизотропного тела можно определить тепловое сопротивление R₀ между центром тела и его поверхностью. Формула для расчета R₀, полученная в результате решения дифференциального уравнения теплопроводности, характеризующего температурное поле однородного анизотропного параллелепипеда, записывается в виде

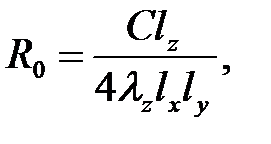(1)

где 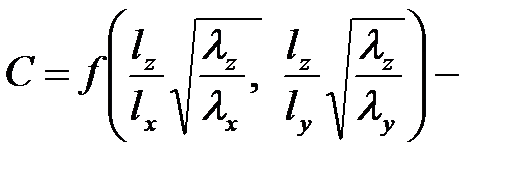коэффициент, характеризующий форму однородного анизотрапного тела, значение которого обычно представляют графически (рис.2). Графики построены для определенных условий выбора направлений осей координат однородного тела. Такими условиями являются неравенства:

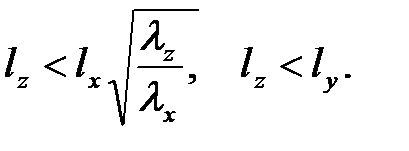
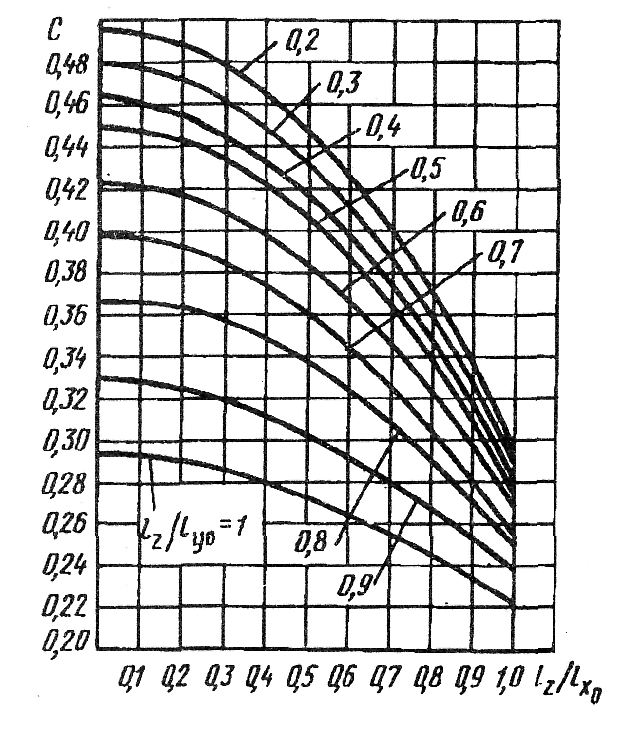
Рис.2 Графики для определения коэффициента формы однородного анизотропного тела

Знание R₀ позволяет найти температуру в центре однородного тела как

t₀ = t_S + R₀ P,

где t_S - температура на поверхности тела; P – суммарный тепловой поток внутренних источников тепла.

Наиболее важным шагом в построении тепловой модели конструк­ции

ЭС в виде однородного анизотропного тела является выделение в конструкции элементарной тепловой ячейки, которая должна отвечать следующим требованиям:

иметь правильную геометрическую форму (желательно форму пря­моугольного параллелепипеда);

обеспечить геометрическую воспроизводимость моделируемой конструкции формальным наращиванием числа ячеек по осям х , у и z ;

допускать представление ячейки совокупностью простейших однородных изотропных тел правильной геометрической формы, для которых достаточно просто рассчитываются тепловые проводимости (сопротивления).

Как правило, в элементарную тепловую ячейку включают источник тепла (радиоэлемент), часть несущей конструкции (основания, печатной платы и т.д.) и воздушных прослоек, окружающих источник тепла.

Процедура выбора элементарной тепловой ячейки иллюстрируется на примере фрагмента конструкции нагретой зоны блока (рис. 3, а)с горизонтально расположенными платами 2, на которых в правильном порядке размещены корпусированные интегральные микросхемы 1. Проекция элементарной тепловой ячейки на координатную плоскости хОу ограничена пунктирной линией и заштрихована.

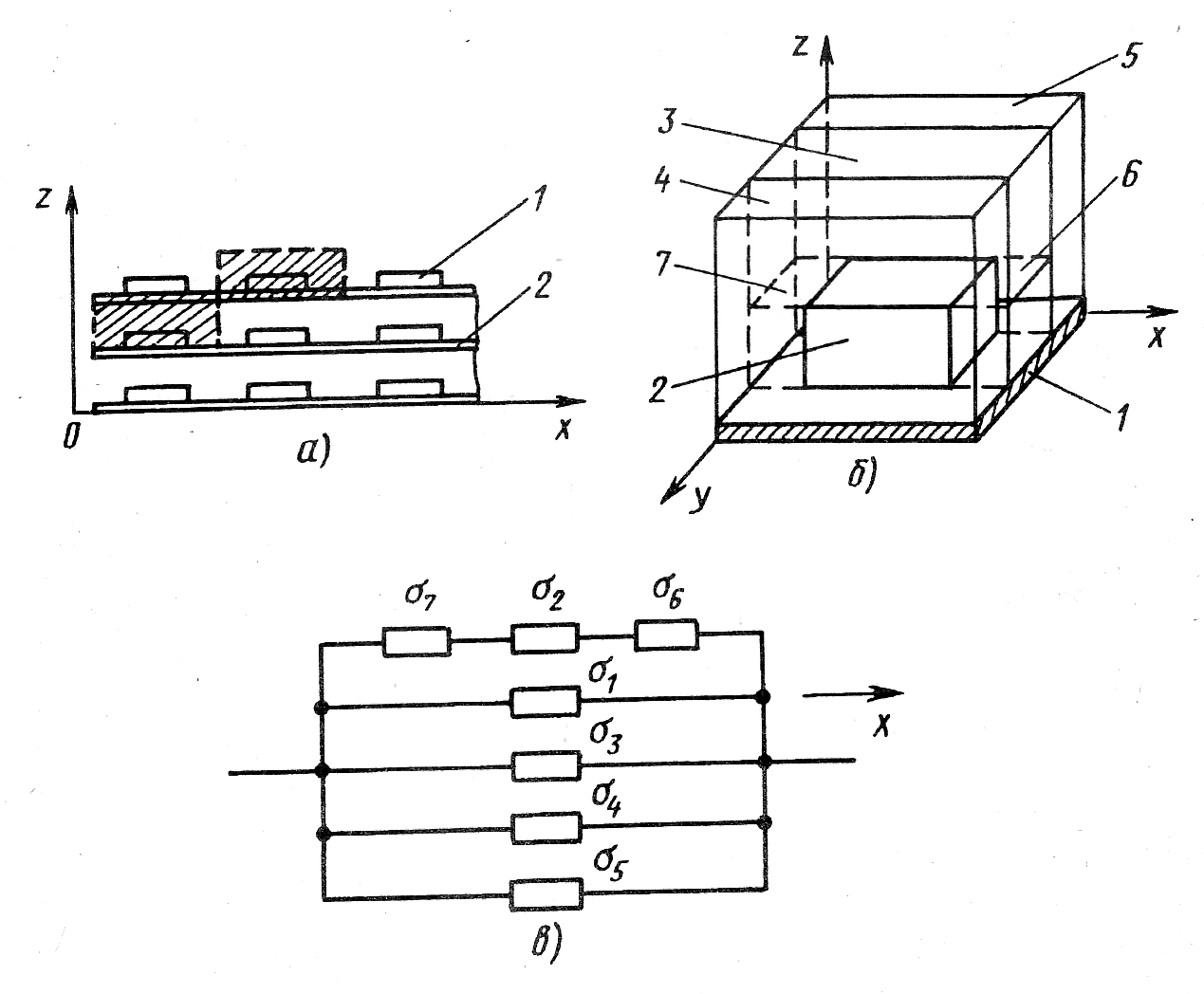
Рис.3 Построение тепловой модели методом однородного анизотропного тела:

а — выделение элементарной тепловой ячейки; б — представление ее структуры; в — тепловая схема ячейки по направлению х

Объемное изображение элементарной тепловой ячейки в увеличен­ном масштабе дано на рис. 3,б. Здесь же показано разбиение ячейки на простейшие составляющие однородные изотропные тела. Как видно из рисунка, все выделенные тела представляют собой прямоугольные параллелепипеды, для которых при известных коэффициентах теплопроводности материала λ, и геометрических размерах тепловая прово­димость может быть найдена по формуле

σ_т= λ S/l, (2)

где S — площадь грани параллелепипеда, перпендикулярной направ­лению теплового потока; l — длина стороны параллелепипеда, совпадающая с направлением теплового потока.

После выделения элементарной тепловой ячейки и ее разбиения на простейшие однородные изотропные тела на основе электротепловой аналогии составляются тепловые схемы, отражающие процесс перено­са тепла в ячейке по направлениям осей координат. На рис. 3, в при­ведена тепловая схема передачи тепла в элементарной тепловой ячейке по направлению х. Индексы тепловых проводимостей на схеме совпада­ет с номерами простейших однородных тел, на которые разбита эле­ментарная тепловая ячейка (см. рис. 3,б). Тепловые схемы отражаю­щие передачу тепла в ячейке по направлениям у и z, построены аналогично и приведены на рис. 4.

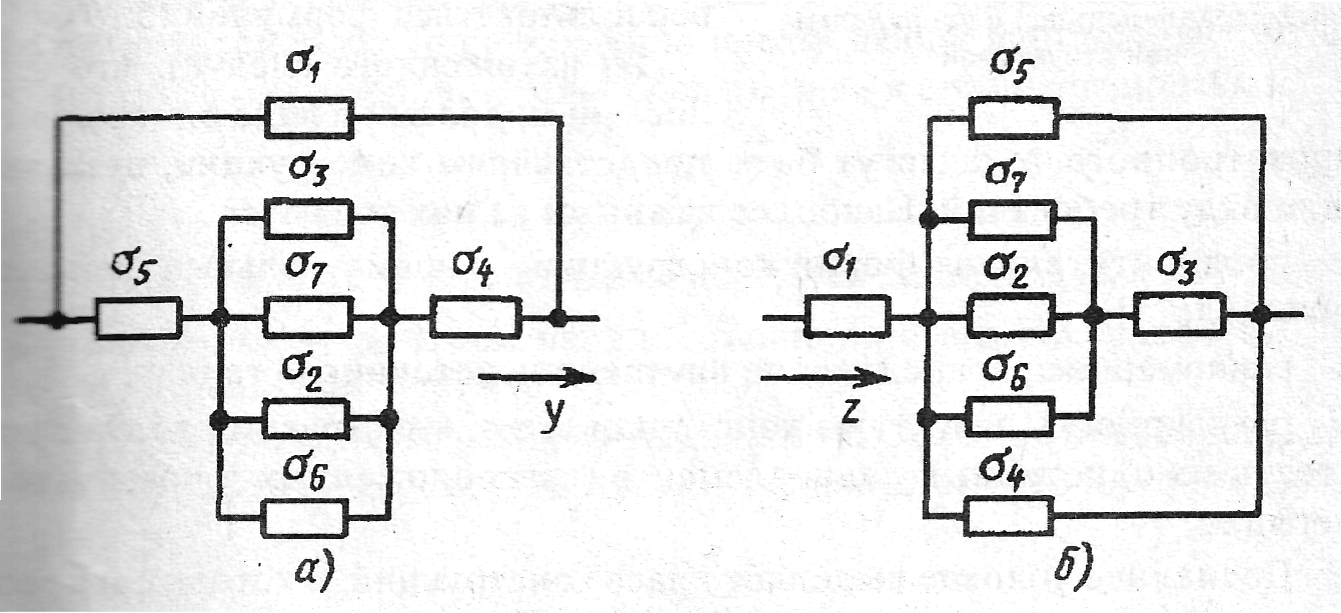
Рис.4 Тепловые схемы элементарной тепловой ячейки по направлениям y (а) и z (б)

Расчет тепловых проводимостей σ₁ ,… σ₇ и преобразование тепловых схем элементарной тепловой ячейки к простейшему виду позволяет найти тепловые проводимости ячейки σ_ях , σ_яy , σ_яz по соответствующим направлениям осей координат.

Завершающим этапом построения тепловой модели является расчет тепловых проводимостей однородного анизотропного тела по направлениям x, y, z и эквивалентных коэффициентов теплопроводности λ_x , λ_y , λ_z . Если однородный анизотропный параллелепипед имеет размеры l_x , l_y , l_z , в пределах которых укладываются соответственно k, m, n элементарных тепловых ячеек (рис.5), то тепловые проводимости параллелепипеда могут быть найдены по формулам:

σ_x = σ_ях mn/k, σ_y = σ_яy kn/m, σ_z = σ_яz km/n.

Эквивалентные коэффициенты теплопроводности находят по формуле (2) через значения σ_x , σ_y , σ_z и геометрические размеры параллелепипеда:

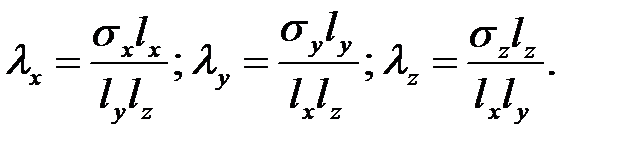
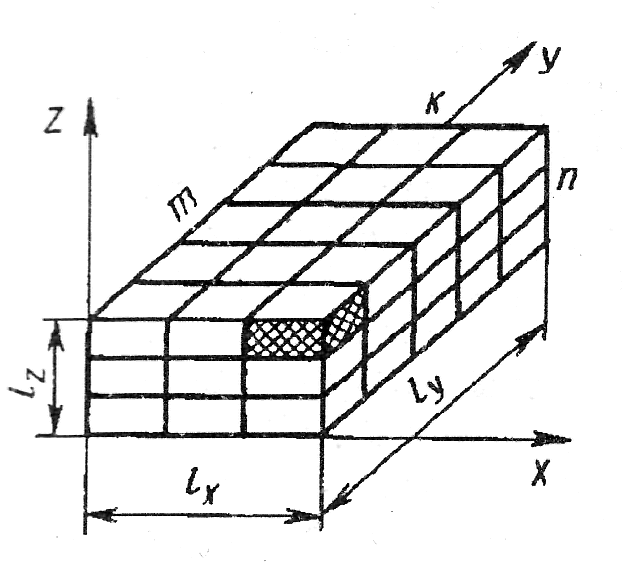
Рис.5 Однородный упорядоченный анизотропный параллелепипед с упорядоченной структурой

После того, как коэффициенты теплопроводности однородного анизотропного тела определены, можно воспользоваться формулой (1).

Из изложенного следует, что тепловыми моделями в виде однородного анизотропного тела могут быть представлены конструкции, отвечающие ряду требований. Наиболее важными из них являются:

предпочтительная форма конструкции — прямоугольный параллелепипед;

равномерное распределение внутренних источников тепла;

регулярность структуры конструкции, т.е. конструкция должна стоять из однотипных радиоэлементов, расположенных в правильном порядке.

Последнее условие выделяет класс конструкций, в которых как геометрические, так и теплофизические свойства периодически повторяются (системы с «дальним порядком»). В таких конструкциях четко обозначены границы элементарной тепловой ячейки, что позволяет без особых затруднений определить параметры тепловой модели. Лучше других данному требованию удовлетворяют конструкции цифровых ЭС разъемного и книжного типов. Тем не менее, даже в этих конструкциях свойство дальнего порядка может частично нарушаться, поскольку не все радиоэлементы имеют одинаковые геометрические формы, не всегда соблюдается периодичность их расположения.