Основные законы излучения.

Закон Планка.Характер изменения интенсивности излучения в зависимости от длины волны и температуры устанавливается ос­нованным на квантовой теории законом Планка.

Для абсолютно черного тела эта зависимость определяется выра­жением:

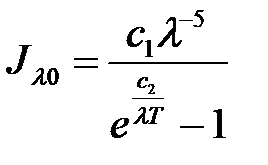, (1)

где с₁ ≈ 3,74 ·10^-16 Вт·м²; с₂≈ 1,44·10 ^-2 м·К.

Из этого уравнения следует, что абсолютно черное тело излуча­ет в любом диапазоне длин волн. При этом интенсивность излуче­ния равна нулю при длинах волн λ,равных нулю и бесконечности, а также при Т₀= 0 К. Теория и практика свидетельствуют о том, что интенсивность излучения J_λ с увеличением λ, растет от нуля до некоторого максимума, после чего вновь уменьшается до нуля (рис. 2).

Закон Вина.Из сравнения полученных при разных температу­рах спектров излучения видно, что длина волны λ_max, соответствую­щая максимальному значению интенсивности излучения, зависит от температуры. Чем выше температура тела, тем меньше λ_max (см. рис. 2). Это положение математически описывается законом сме­щения Вина:

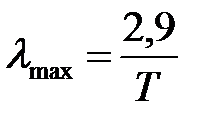(mm). (2)

В отличие от абсолютно черного тела неокисленные чистые ме­таллы и газы излучают энергию в узком диапазоне длин волн. Такое излучение называется селективным.

Закон Ламберта.Согласно закону Ламберта, количество лучистой энергии, излучаемой элементом рассеивающей поверхности под уг­лом φ к нормали (рис. 3), равно произведению количества энергии, излучаемой по нормали, на косинус угла φ: Е_φ = Е_п · cosφ, где Е_п — плотность потока излучения, называемая также яркостью. В соот­ветствии с этим законом наибольшее количество энергии излучает­ся по нормали к излучающей поверхности. Закон Ламберта неприменим к полированным металлам.

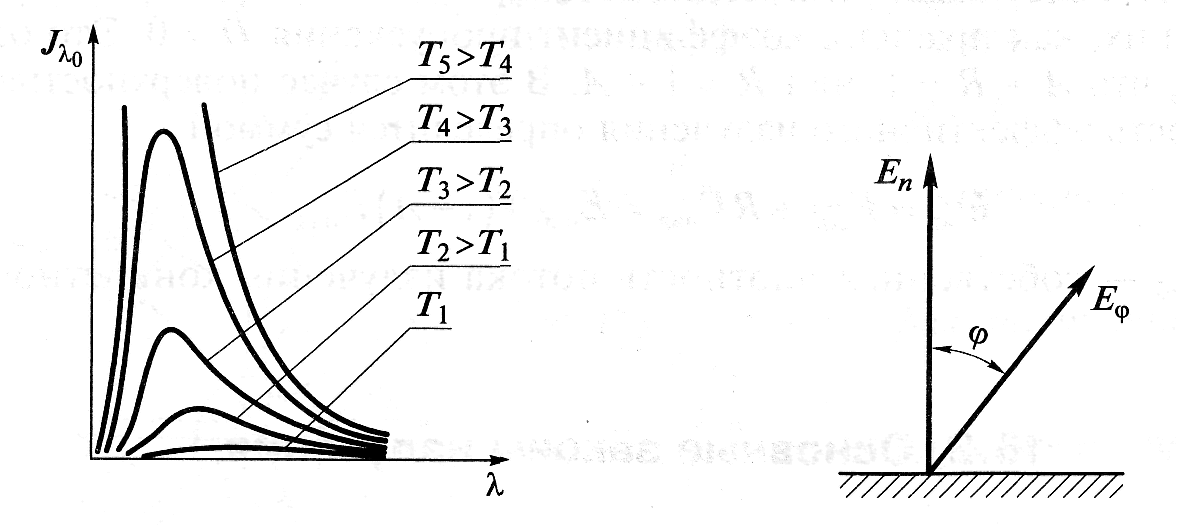
Рис.3 Зависимость интенсив- Рис.4 Излучение рассеивающей

ности излучения АЧТ от длины поверхности

волны и температуры

Закон Стефана-Больцмана. С использованием выражения (1) может быть получена формула для определения поверхностной плот­ности Е₀ абсолютно черного тела:

Е₀=σ₀Т⁴. (3)

В этом уравнении коэффициент σ₀ = 5,67·10^-8 (Вт/(м²·К⁴) назы­вается постоянной излучения Стефана-Больцмана. Для технических расчетов уравнение закона Стефана-Больцмана удобнее записывать в виде

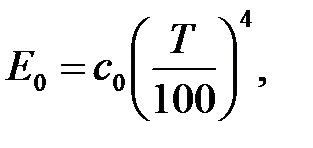(4)

где с₀ — коэффициент излучения АЧТ: с₀ = 5,67 Вт/(м² ·К⁴).

Спектр излучения реальных тел отличается от спектра АЧТ. На­пример, для газов он может иметь даже полосовой характер, когда излучение происходит в узких диапазонах длин волн. При этом ис­пользование уравнения (4) приводит к погрешностям.

Для удобства рассмотрения излучения реальных тел вводят по­нятие серых тел. Эти тела имеют непрерывный спектр излучения, аналогичный спектру АЧТ, и отношение интенсивности излучения серого тела на каждой длине волны к соответствующей интенсив­ности излучения АЧТ при одинаковой температуре есть величина постоянная. Это отношение называется степенью черноты:

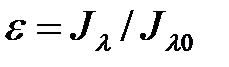. (5)

После интегрирования этого выражения от λ = О до λ= ∞ по­лучим

ε = Е/Е₀. (6)

Для серого тела закон Стефана-Больцмана имеет вид:

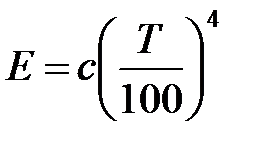,(7)

где с = ε с₀ — коэффициент излучения серого тела (поскольку степень черноты в соответствии с формулой (6) может быть представлена как ε = с/с₀).

Степень черноты и коэффициент излучения реального серого тела зависят от его температуры, но зависимость эта незначительна.

Закон Кирхгофа.При теплообмене между бесконечно большой абсолютно черной поверхностью и расположенной близко от нее поверхностью серого тела (рис. 5) черное тело будет поглощать всю теплоту, попадающую на него от серого тела. Серое же тело поглощает лишь часть АЕ₀ излучаемой в его сторону тепловой энер­гии, а другая часть, равная (1 - А)Е₀, будет им отражаться на абсо­лютно черную поверхность.

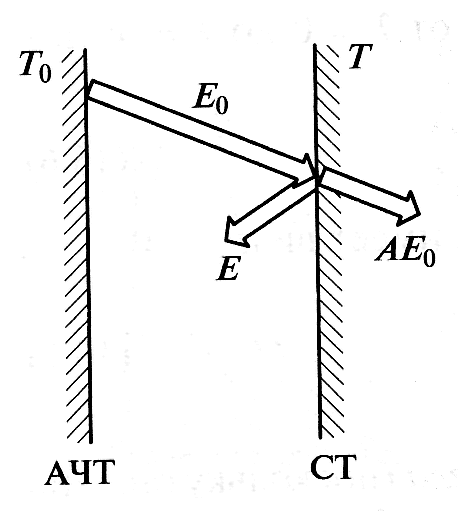
Рис. 5 Теплообмен между параллельными абсолютно черной и серой плоскостями

В случае равенства температур поверх­ностей должен соблюдаться тепловой баланс (каждое из тел погло­щает и излучает одинаковое количество теплоты), а потому можно записать

Е = АЕ₀ , (8)

где Е — плотность теплового потока, излучаемого серым телом; АЕ₀ — часть тепловой энергии, поглощаемая его поверхностью. Это равенство можно представить в виде

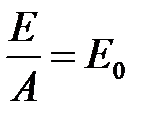. (9)

Это уравнение справедливо для любых серых тел. Сформулиро­ванный на его основе закон Кирхгофа устанавливает, что при оди­наковых температурах отношение излучаемой энергии серого тела к поглощаемой им энергии есть величина постоянная и равная энер­гии, излучаемой абсолютно черным телом при рассматриваемой температуре. Иными словами, чем больше тело поглощает, тем боль­ше оно излучает, и наоборот.

Из формулы (8) следует, что 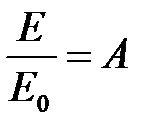. Сравнивая с выражением (6) и подставляя значения Е и Е₀, получаем

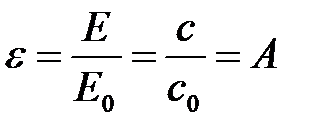. (10)

Отсюда следует, что численное значение степени черноты εсерого тела равно его ко­эффициенту поглощения при той же темпе­ратуре.

Для абсолютно черного тела А = 1, а по­тому Е = Е₀ и с = c₀.