Общая характеристика тепловых моделей ЭС. Тепловые модели.
Как отмечалось выше, ЭС можно рассматривать, как систему многих тел с сосредоточенными источниками тепловой энергии. Анализ температурных полей таких систем является весьма сложной задачей, решение которой выполняется приближенными методами. Исследователь пытается установить количественную зависимость между температурой ограниченного числа наиболее ответственных мест аппарата и существенными факторами, влияющими на процесс теплообмена. Тепловые процессы в реальной конструкции ЭС, как правило, не поддаются математическому описанию из-за наличия большого числа основных и второстепенных факторов, влияющих на процесс. Поэтому необходим переход к тепловой модели ЭС.
В настоящее время получили развитие две группы тепловых моделей ЭС. Характерной особенностью моделей первой группы является разделение всех поверхностей модели ЭС на отдельные условно изотермические участки. Например, при определении среднеповерхностной температуры нагретой зоны условно изотермическими считаются поверхность корпуса и вся поверхность нагретой зоны, состоящая из поверхностей элементов и части шасси, не занятой ими.
На рис. 1, а схематически показан разрез электронного аппарата и указаны значения температур, измеренных в разных точках корпуса, шасси и радиодеталей. На рис. 1, б представлена тепловая модель того же аппарата, на основании которой определяются среднеповерхностные температуры его нагретой зоны и корпуса. При этом сложная по форме нагретая зона реального аппарата заменена прямоугольным параллелепипедом, поверхность которого рассматривается как изотермическая. Такое же допущение делается относительно температурного поля корпуса. Задача упрощается настолько, что математическое описание процесса теплообмена в тепловой модели аппарата становится возможным и сравнительно несложным.
На рис. 2, а схематически изображен разрез радиоэлектронного аппарата кассетной конструкции, на монтажных платах (кассетах) которого смонтированы модули, микросхемы, микромодули и т. д. Значения температур корпуса и отдельных точек нагретой зоны не указаны, но предполагается, как и в первом примере, что поля температур неравномерны. К такому радиоэлектронному аппарату можно применить тепловую модель рис. 1, б и описать процессы переноса тепла от поверхности нагретой зоны к корпусу и далее в среду. В результате анализа получим средние поверхностные температуры корпуса и нагретой зоны.
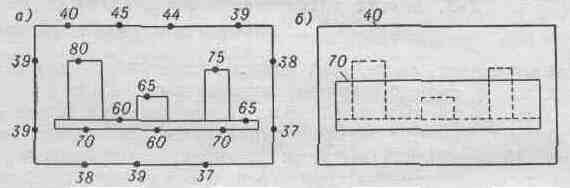
Рис. 1 Разрез простейшей конструкции ЭС (а) и его тепловая модель (б)
Для анализа температурного поля внутри нагретой зоны существуют следующие возможности:
1. Каждая плата с деталями представляется в виде пластины с равномерно распределенным источником тепла мощностью Pi и равномерным полем температур (рис. 2, б) и рассматриваются процессы теплообмена, протекающие между изотермическими поверхностями. В этом случае информация о тепловом режиме становится более полной: возможно определить не только среднюю температуру внешней поверхности нагретой зоны и корпуса, но и средние значения температур каждой платы.
2. Если источники энергии заметно изменяются по высоте платы или условия теплообмена одной части платы по каким-либо причинам резко отличны от другой части той же платы, то следует провести более подробную разбивку, как это показано на рис. 2, в, и вместо семи изотермических поверхностей рис. 2, б (одна поверхность — корпус, шесть — платы) ввести, например, 16 изотермических поверхностей. Информационные возможности тепловой модели рис. 2, в значительно больше, чем модели рис. 2, б; изучая модель рис. 2, в, можно определить среднеповерхностные температуры шестнадцати поверхностей. Процессы переноса тепла в тепловых моделях первой группы рассматриваются так, как если бы они протекали между изотермическими поверхностями.
В тепловых моделях, относящихся ко второй группе, нагретая зона ЭС, представляющая собой неоднородную систему многих тел, идеализируется в виде однородного тела. Свойства этого тела характеризуются эффективными значениями коэффициентов теплопроводности l, теплоемкости с.
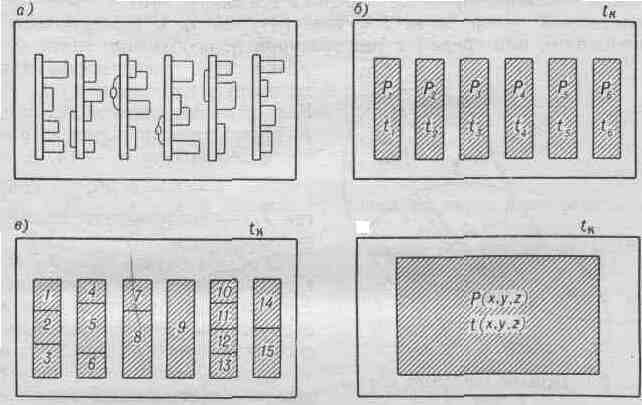
Рис. 2. Разрез аппарата кассетной конструкции (а) и его тепловые модели (б, в, г)
На рис. 2, г изображена тепловая модель второй группы для аппарата, изображение которого приведено на рис. 2, а. Нагретая зона аппарата представляет собой совокупность многих тел с дискретными источниками тепловой энергии. В тепловой модели нагретая зона — однородное анизотропное тело с распределенным по объему источником энергии. Ее исследование позволяет получить аналитическое выражение для поля температур нагретой зоны.
Особенности тепловых моделей ЭС определяют математический аппарат, применяемый для их анализа. Тепловые модели первой группы исследуются при помощи так называемого метода тепловых схем, который позволяет описать процессы переноса тепла в ЭС при помощи системы неоднородных нелинейных алгебраических уравнений. Для изучения тепловых моделей второй группы применяются дифференциальные уравнения теплопроводности. При исследовании теплового режима сложных конструкций тепловая модель аппарата может содержать в себе элементы обеих указанных групп моделей. При этом отдельные части сложных ЭС представляются в виде условно изотермических поверхностей, другие - в виде однородных тел.
Сравнение эффективности различных способов охлаждения.
Эффективность того или иного способа охлаждения определяется интенсивностью протекающих процессов теплообмена. Чем интенсивнее теплообмен, тем эффективнее способ охлаждения. Известно, что интенсивность теплообмена определяется величиной коэффициента теплообмена. В таблице приведены ориентировочные значения этих коэффициентов в (Вт/м2 *град) для различных видов теплообмена.
| Естественная конвекция и излучение | 2 -10 |
| Вынужденная конвекция в воздухе и газах | 10-100 |
| Естественная конвекция в масле и других жидкостях той же плотности | 200 - 3000 |
| Вынужденная конвекция в масле и других жидкостях той же плотности | 300 - 1000 |
| Естественная конвекция в воде | 200 - 600 |
| Вынужденная конвекция в воде | 1000 - 3000 |
| Кипение воды | 500 - 45000 |
| Капельная конденсация водяных паров | 40000 - 120000 |
| Конденсация органических паров | 500 - 2000 |
1. Теплопроводность. Тепловые коэффициенты.
Теплопроводностью (кондукцией) называют перенос тепловой энергии при соприкосновении частиц вещества или отдельных тел, имеющих разные температуры. Процесс передачи тепловой энергии теплопроводностью обычно связывают с твердыми телами, но при определенных условиях он наблюдается также в жидкостях и газах.
При математическом описании процесса теплопередачи принято считать, что теплообмен происходит между изотермическими поверхностями, причем изотермическая поверхность с большей температурой отдает тепло изотермическим поверхностям с меньшей температурой.
Для описания процесса переноса теплового потока Pi от изотермической поверхности i с температурой ti к изотермической поверхности или среде j с температурой tj, необходимо знать аналитическую зависимость, связывающую параметры ti, tj, Pi .(Как известно, тепловой поток Pi прямо пропорционален разности температур (ti — tj ), т. е.
ti — tj = FijPi(1)
где Fij— коэффициент пропорциональности.
В общем случае Fij= Fij(ti, tj ).
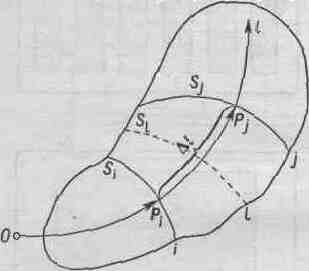
Рис.1 Перенос теплового потока в теле
Дата добавления: 2016-07-05; просмотров: 3522;











