Тепловые коэффициенты и тепловые сопротивления

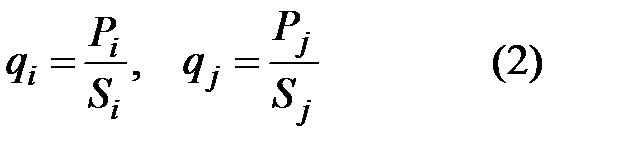
На рис. 1 изображено сечение сплошного тела и показаны следы двух изотермических поверхностей S_i, S_j, имеющих температуры в данный момент времени t_i,, t_j,. Линии, перпендикулярные к изотермическим поверхностям, являются линиями теплового потока, на рис. 1 эти линии обозначены стрелками. Через единицу площади изотермической поверхности проходит тепловой поток q, который называется удельным тепловым потоком, или плотностью теплового потока; например, плотности тепловых потоков через поверхности iиjравны:

Теплообмен кондукцией происходит согласно закону Фурье: плотность теплового потока q прямо пропорциональна градиенту температуры, т. е.

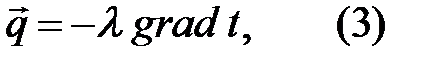
где l — коэффициент теплопроводности материала; 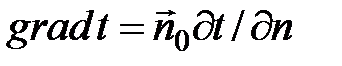— градиент температуры.

Напомним, что за положительное направление градиента температуры принимают направление, в котором температура возрастает.

Запишем закон Фурье для некоторой изотермической поверхности S_l, находящейся между поверхностями i и j (рис. 1). Буквой l обозначена координата поверхности S_l, отсчет ведется от какой-либо точки 0, координатная линия l совпадает с линией тока. Тогда выражение (3) можно записать в виде

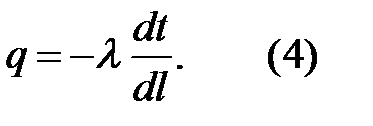
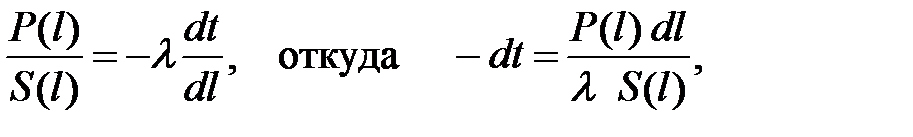
Объединим зависимости (2) и (4):

где Р (l) — величина потока, через изотермическую поверхность S (l).

Произведем интегрирование последнего выражения от t_i до t_j :

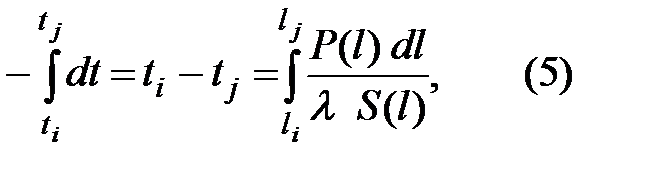
где l_i и l_j — координаты изотермических поверхностей i и j.

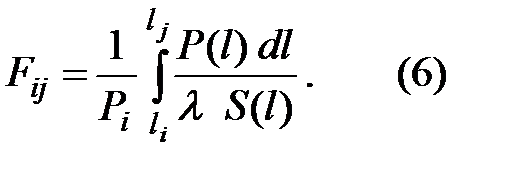
Сравнивая выражения (1) t_i — t_j = F_ijP_i и (5), получим структуру коэффициента пропорциональности F_ij при кондуктивном переносе тепловой энергии:

Если между изотермическими поверхностямиiиj отсутствуют стоки или источники энергии, то Р(l) не изменяется на пути между этими поверхностями, т. е. Р (l) =P_i = const, то F_ij - называется тепловым сопротивлением, обозначается R_ij и выражение (6) приобретает вид

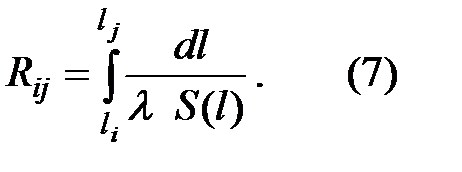
Заметим, что источниками энергии могут быть дискретные или распределенные между i и j источники джоулева тепла; стоки энергии могут быть обусловлены эффектом Пельтье, химическими реакциями и т. п. К стокам энергии можно также отнести потери тепла на границах тела между изотермами iи j.

Величина, обратная тепловому сопротивлению, называется тепловой проводимостью:

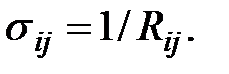(8)

Если S, λ = const, то

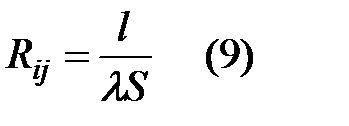
Известная зависимость для теплового потока в конечных разностях принимает вид:

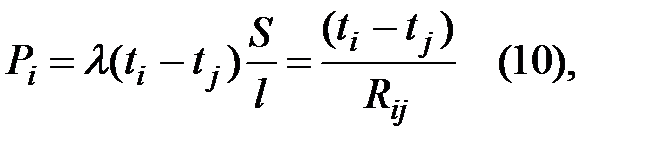
или разность температур можно найти как

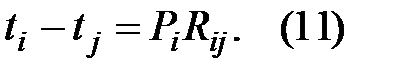
2. Уравнения теплопроводности и краевые условия.

Предположим, что температурное поле изменяется только в направлении x (рис.2).

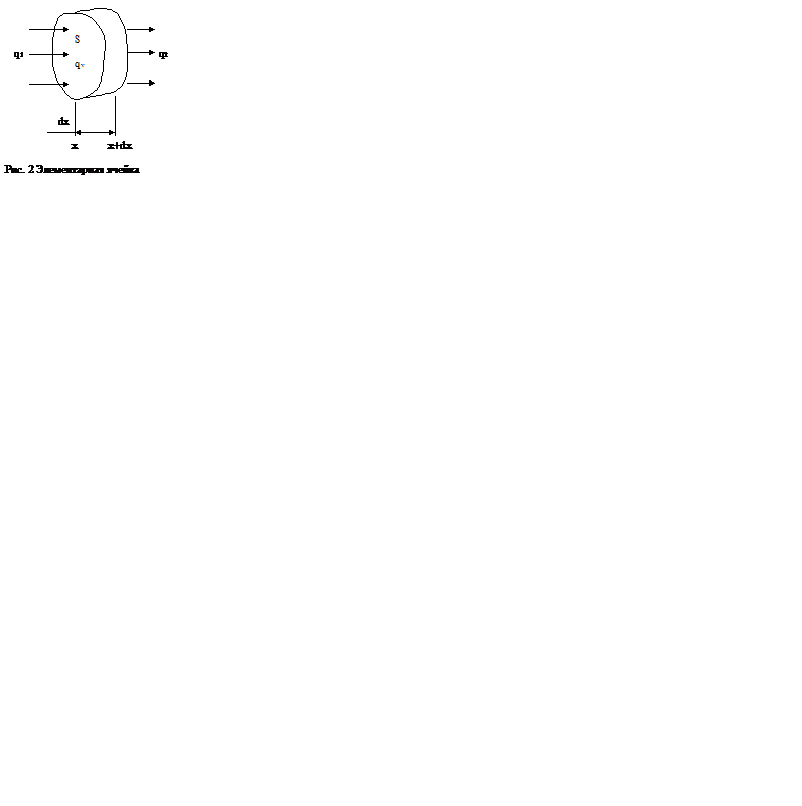
Рассмотрим элементарный объем dV = S*dx, где S – площадь, а dx – толщина элементарного объема. (Например, участок электрического кабеля). Пусть q₁ –плотность теплового потока в сечении x, а q₂ -в сечении x+dx; если dx мало, то в первом приближении изменение теплового потока в направлении оси x описывается двумя членами разложения q₁ в ряд Тейлора:

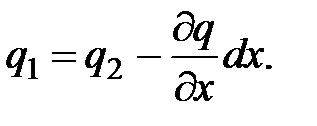
Найдем разность Q между входящими и выходящими количествами теплоты через поверхности S за время dτ:

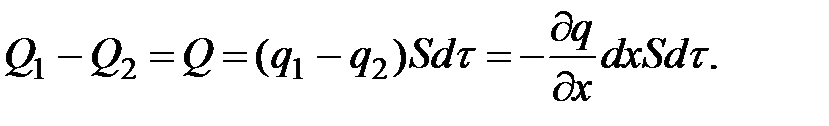
Сформулируем закон сохранения энергии для рассматриваемого элемента.

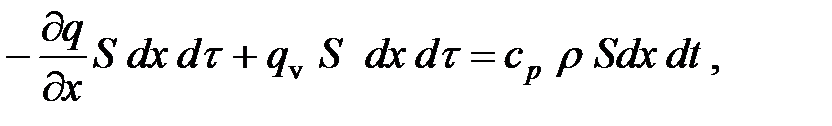
Количество теплоты Q вместе с энергией Q_v= q_v dx S dτ внутренних источников расходуется на изменение температуры dt объема Sdx:

где q_v- объемная плотность теплового потока, Вт/м³; c_p- удельная теплоемкость при постоянном давлении; ρ – плотность материала;

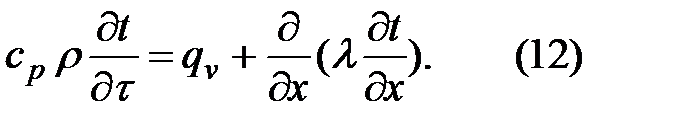
Подставим в последнее уравнение значение q из формулы Фурье (4) и после преобразований получим уравнение теплопроводности

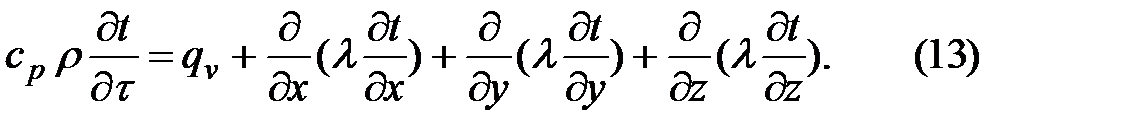
Для трехмерного тела уравнение принимает вид

Для анизотропного тела в направлении осей x, y, z теплопроводности λ_x, λ_y, λ_z имеют различные значения и дифференциальное уравнение принимает вид

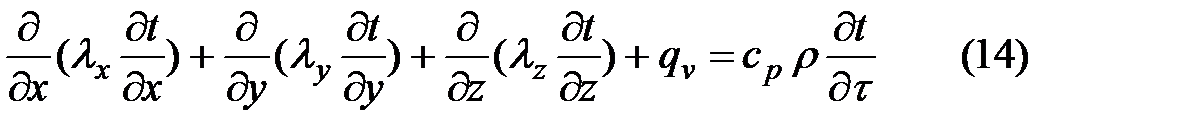
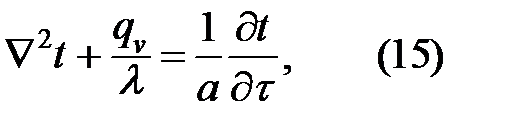
Для изотропного тела λ_x, λ_y, λ_z равны λ и уравнение теплопроводности переписывается в виде

где a=λ/(c_p ρ)- коэффициент температуропроводности вещества;

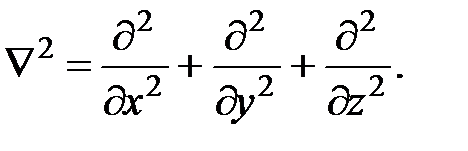
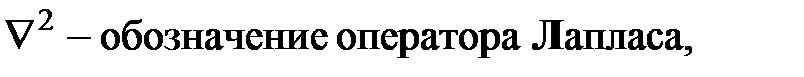
В стационарном режиме (∂t/∂τ=0) уравнение принимает вид

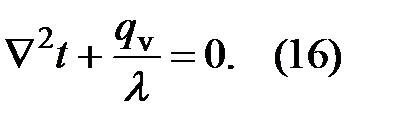
Если внутренние источники тепла отсутствуют, то

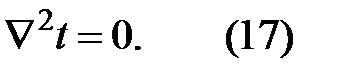
Путем преобразования системы координат дифференциальное уравнение для анизотропных тел (14) можно записать в форме (15).

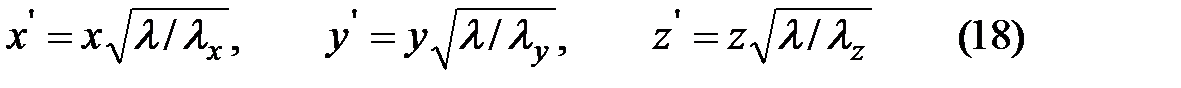
В зависимостях (18) λ - так называемая базовая теплопроводность, выбор которой произволен; обычно за λ принимают одно из трех значений теплопроводностей: λ_x, λ_y, или λ_z. Произведем некоторые преобразования и подставим новые значения координат (18) в уравнение (15)

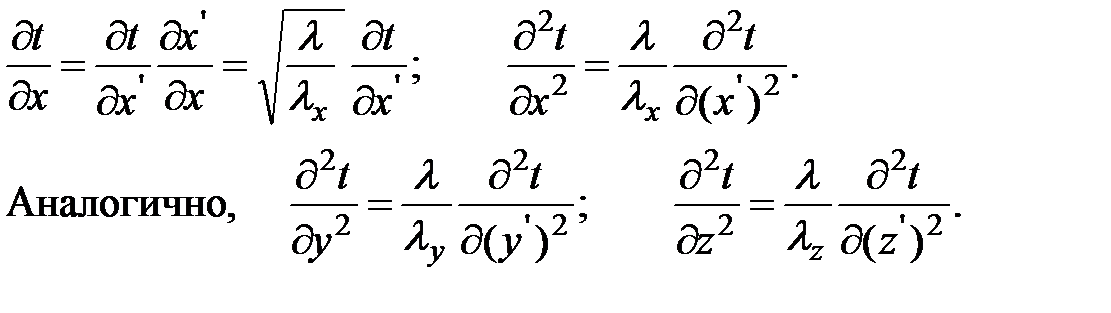
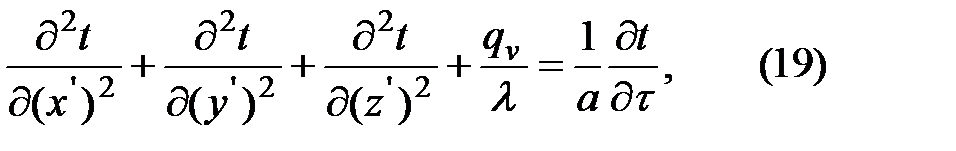
Уравнение (14) после преобразований принимает вид аналогичный по форме (15).

Краевые условия. Для решения дифференциального уравнения необходимо задать условия однозначности. Они включают в себя:

- граничные условия (ГУ), определяющие характер тепловых связей рассматриваемого тела с соседними телами и средой;

- в случае нестационарной задачи (∂t/∂τ ≠0) необходимо знать начальные условия, т.е значение температурного поля t₀(x, y, z) в начальной точке времени τ = τ₀ рассматриваемого процесса.

Существует четыре вида ГУ.

· ГУ 1 рода (задача Дирихле). Задается распределение температур на поверхности тела для каждого момента времени t_s = f(x, y, z, τ). В частном случае t_s =const.

·
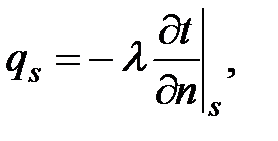
ГУ 2 рода (задача Неймана). Задано распределение плотности теплового потока в любой момент времени q_s = f(x, y, z, τ):

где -λ(∂t/∂n) - плотность теплового потока, уходящего вглубь тела.

· ГУ 3 рода. Задана температура окружающей среды t_c и закон теплообмена между поверхностью тела и окружающей средой. На основании закона Ньютона - Рихмана плотность теплового потока на границе тело-среда

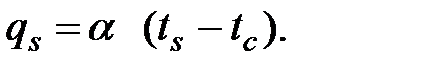
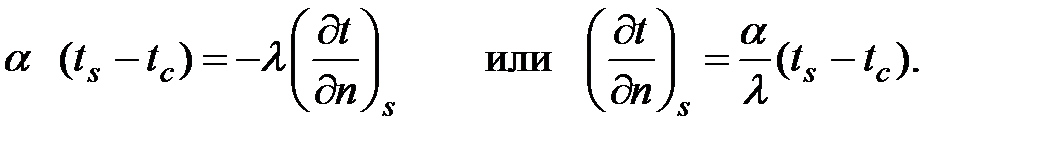
К поверхности тела за счет теплопроводности подходит тепловой поток, плотность которого определяется законом Фурье. Если на границе раздела отсутствуют источники или стоки энергии то

·
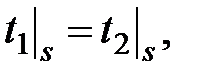
ГУ 4 рода. Характеризуют граничные условия в виде теплового контакта между твердыми телами при идеальном контакте между ними. Математическая формулировка ГУ 4-го рода при отсутствии источников или стоков тепла на границе раздела заключается в следующем:

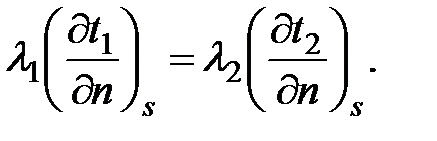
Дифференциальное уравнение теплопроводности и его условия однозначности дают полную математическую формулировку задачи.

3. Конвективный перенос тепла. Основы теории подобия.

Теплообмен между поверхностью S твердого тела и окружающей его жидкой или газообразной средой подчиняется закону Ньютона—Рихмана:

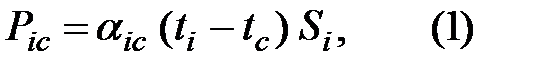
где Р_ic—тепловой поток от поверхности твердого тела к среде;

S_i — площадь поверхности теплообмена тела; α_ic — коэффициент теплообмена между поверхностью тела и средой;t_iи t_c — температуры поверхности тела и среды.

Вспомним, что t_i — t_j = F_ijP_i , отсюда находим структуру теплового коэффициента F_ic = 1/ α_ic S_i. Если между поверхностью тела и окружающей его средой отсутствуют источники или стоки энергии, то величина теплового потока Р_ic при движении от изотермической поверхности с температурой t_i к среде с температурой t_j не изменяется и поэтому F_ic можно считать тепловым сопротивлением, т. е.

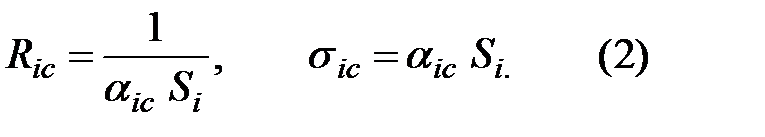
Вся сложность процесса конвективного теплообмена концентрируется в одной величине — коэффициенте теплоотдачи α, который представляет собой функцию большого числа параметров, существенно влияющих на процесс теплообмена. Прежде всего конвективный теплообмен оказывается связанным с движением самой жидкости, т. е. с гидродинамическим процессом.

В 1883 г. английский ученый Осборн Рейнольдс показал, что существуют два основных режима движения жидкости: ламинарный и турбулентный. При ламинарном движении отдельные струи потока располагаются параллельно друг другу, тогда как при турбулентном они хаотически переплетены друг с другом.

На рис. 1, а схематически показана модель движения жидкости вдоль пластины, включающая два режима течения — ламинарный и турбулентный. На переднем участке пластины х<х_кр образуется ламинарный гидродинамический пограничный слой толщиной δ_л(x). Гидродинамическим пограничным слоем называют пристенный слой жидкости толщиной δ, в котором происходит изменение скорости движения жидкости от нулевой (на поверхности тела) до значения V₀— скорости основного потока жидкости.

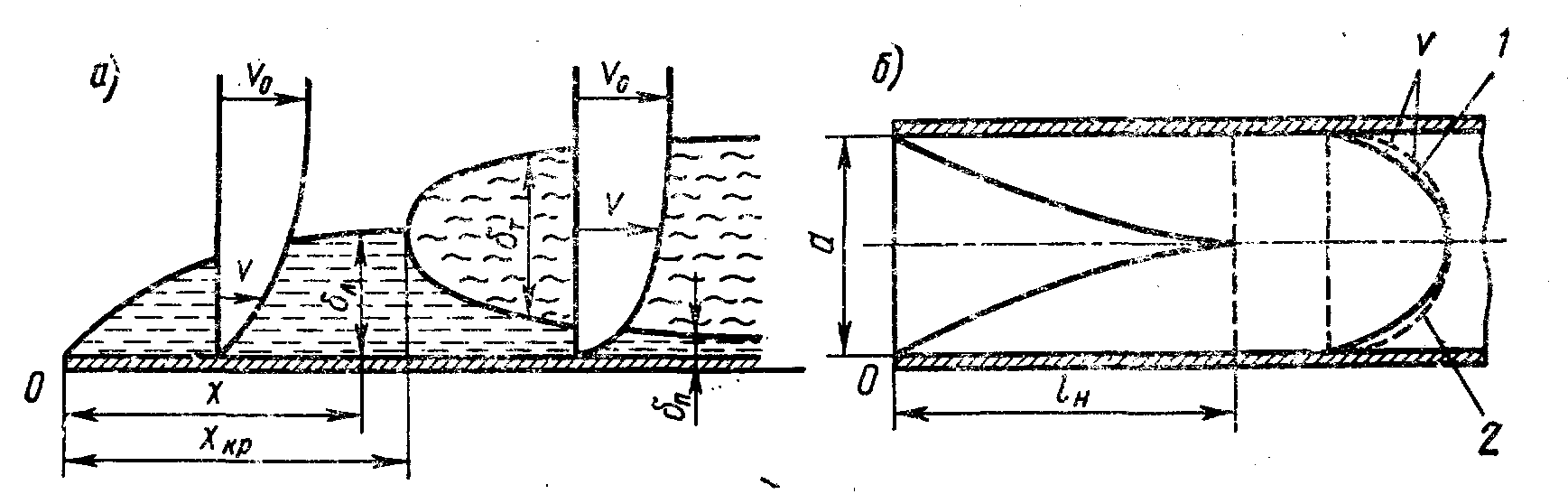
Рис. 1. Структура пограничного слоя: а — обтекание пластины потоком жидкости; б — течение жидкости в трубе

Переход из турбулентного течения в ламинарное и обратно количественно характеризуется так называемым числом Рейнольдса — Re. Например, при обтекании пластины при значении числа Рейнольдса Re = VL/ν >5*10⁵ возникает турбулентность.

Типичные модели конвективного теплообмена — это движение жидкости вдоль пластины, свободная конвекция у вертикальной пластины, течение жидкости в канале.

Как только x ≥x_крстановится больше критической, движение в слое становится неупорядоченным, вихревым; образуются турбулентный пограничный слой толщиной δ_т и ламинарный подслой толщиной δ_п .

У внутренней поверхности трубы образуется пограничный слой, толщина которого у входного края трубы равна нулю, а затем постепенно возрастает, как это показано на рис. 1, б. На определенном расстоянии х>l_н от входа пограничный слой утолщается настолько, что заполняет все сечение, начинается область стабилизированного течения. Кривая распределения скорости потока по сечению канала имеет форму параболы 1 (ламинарное движение) либо более сложной выпуклой кривой 2(турбулентное движение). Для. стабилизированного потока, как будет показано ниже, при Re = Vd/ν ≥2300 ламинарное течение переходит в турбулентное.

Ниже для различных случаев теплообмена приведены значения коэффициентов теплоотдачи α: