Привод шлагбаума ША-8N

Цилиндрические открытые зубчатые передачи рассчитываются аналогично закрытым. Методика расчёта соответствует ГОСТ 21354-87 "Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность".

Особенность расчёта обусловлена спецификой работы таких передач. Они не защищены или очень слабо защищены от попадания абразивных частиц из окружающего воздуха, не имеют постоянного смазывания, а часто и вообще работают без смазки. Поэтому они главным образом используются в тихоходных механизмах, работающих периодически, с большими перерывами: ручных лебёдках, тельферах и т.п.

Основными видами разрушения открытых зубчатых колес является поверхностный износ, искажающий форму зубьев и уменьшающий его поперечное сечение, что ведёт к поломке зубьев от действия переменных напряжений при изгибе. усталостное выкрашивание поверхностей зубьев от действия переменных контактных напряжений встречается редко. Поэтому проектный расчёт ведётся по изгибным, а проверочный – по контактным напряжениям.

Примером такой передачи может служить тихоходная ступень привода шлагбаумов (рис. 3.8) типа ША (4, 6, 8, N и S), поднимающая и опускающая заградительный брус [37].

- Такая передача хотя и находится в корпусе, но шлагбаум подвержен самым неблагоприятным атмосферным условиям (пыль, песок), к тому же работает периодически, а зубчатое зацепление смазывается при сборке и обслуживании консистентной смазкой, которая под действием температурных условий может пересыхать или стекать с колёс. Кроме того, имеется смотровая заслонка. Всё это позволяет приравнять передачу по условиям работы к открытым.

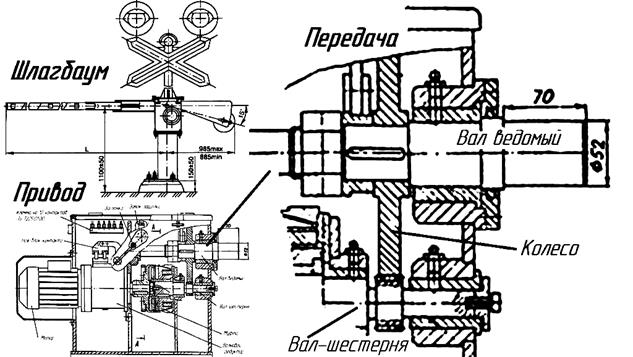
Рис. 3.8. Конструкция привода шлагбаума типа ША

Рассмотрим исходные данные для расчёта передачи.

Передача реверсивная. Привод должен или поднимать заградительный брус из горизонтального положения в вертикальное или опускать его на четверть оборота за 4…5 секунд (примем 4,5 с), это значит, что частота вращения выходного вала передачи n₂ = 3,33 об/мин. Передаточное отношение передачи зададим U = 4, т.е. частота вращения ведущего вала n₁ = n₂·U = 13,32 об/мин.

Вращающий момент на выходном валу требуется M₂ = 500 Нм. Следовательно, на вал заградительного бруса приходит мощность N₂ = π·M₂·n₂/30= = 500·3,14·3,33/30 = 174,3 Вт.

КПД открытой цилиндрической передачи с учётом потерь в подшипниках скольженияпримем η = 0,9. Это значит, что на ведущем валу развивается мощность N₁ = N₂/η = 174,3/0,9 = 193,6 Вт. Это соответствует моменту
M₁ = 30·N₁/(π·n₁) = 30·193,6/(3,14·13,32) = 138,9 Нм.

Ресурс привода 10⁶ циклов подъём-опускание (на 90°). Каждый такой цикл это половина оборота. Таким образом, фактическое число циклов нагружения зубьев колеса N_FE2 = N_НE2 = 0,5·10⁶ циклов (оборотов). Фактическое число циклов нагружения зубьев шестерни N_НE2 = N_FE2 = N_FE1·U = 0,5·10⁶ ∙ 4 =
= 2,0·10⁶ циклов (оборотов).

Колёса расположены симметрично относительно опор.

Кроме того, имеется конструктивное ограничение: привод закреплён на стойке шлагбаума и его габаритная ширина (фактически обусловленная диаметром большего из колёс) не должна быть больше 250 мм.

Расчёт передачи проводим в следующей последовательности [46].

Выбираем материалы колёс (табл. 3.1). Так как заданием не предусматривается специальных требований к массе передачи, выбираем в качестве материала для изготовления зубчатых колёс сталь со средними механическими характеристиками и относительно небольшой стоимостью:

− для шестерни сталь 45, термообработка – улучшение НВ250, модуль упругости E₁ = 2,1·10⁵ МПа, предел контактной выносливости σ_Hlim1 = 1,8∙HB +
+ 65 = 1,8∙250 + 65 = 515 МПа; коэффициент контактной безопасности S_Н1 = 1,1; предел изгибной выносливости σ_Flim1 = 1,8∙HB = 1,8∙250 = 450 МПа; коэффициент изгибной безопасности S_F1 = 1,65;

− для колеса сталь 45, термообработка – нормализация НВ217, модуль упругости E₂ = 2,1·10⁵ МПа, предел контактной выносливости σ_Hlim2 = 1,8∙HB +
+ 65 = 1,8∙217 + 65 = 455 МПа; коэффициент контактной безопасности S_Н2 = 1,1; предел изгибной выносливости σ_Flim2 = 1,8∙HB = 1,8∙217 = 390 МПа; коэффициент изгибной безопасности S_F2 = 1,65;

Передача реверсивная, для обоих стальных колёс коэффициент K_FC = 0,72.

Вычисляем базовое число циклов контактных напряженийN_HO.

для шестерни N_HO1 = 30 НВ^2,4 = 30 · 250^2,4 = 17,06 · 10⁶.

для колеса N_HO2 = 30 НВ^2,4 = 30 · 217^2,4 = 12,15 · 10⁶.

Базовое число циклов изгибных напряженийN_FO1 = N_FO2 = 4·10⁶.

Рассчитываем коэффициенты долговечности (см. разд. 3.2):

K_HL1 = (N_HO1/N_HE1)^1/6 = (17,06·10⁶/2·10⁶)^1/6 = 1,44;

K_HL2 = (N_HO2/N_HE2)^1/6 = (12,15·10⁶/0,5· 10⁶)^1/6 = 1,70;

K_FL1 = (N_FO1/N_FE1)^1/9 = (4·10⁶/2·10⁶)^1/9 = 1,08;

K_FL2 = (N_FO2/N_FE2)^1/9 = (4·10⁶/0,5·10⁶)^1/9 = 1,26.

Вычисляем допускаемые контактные напряжения:

[σ_Н]₁= (σ_Нlim1 /S_H1)·K_HL1 = (515/1,1)·1,44 = 603 МПа,

[σ_Н]₂= (σ_Нlim2 /S_H2)·K_HL2 = (455/1,1)·1,7 = 703 МПа.

Вычисляем допускаемые напряжения при изгибе:

[σ_F]₁ = (σ_Flim1 /S_F1)·K_FC1·K_FL1 = (450/1,65)·0,72·1,08 = 212 МПа,

[σ_F]₂ = (σ_Flim2 /S_F2)·K_FC2·K_FL2 = (390/1,65)·0,72·1,26 = 214 МПа.

Задаём числа зубьев и угол наклона. В виду тихоходности передачи, а также во избежание нагружения осевыми нагрузками подшипников скольжения, принимаем прямозубые колёса. Задаём число зубьев шестерни Z₁ = 17 из условия неподрезания, тогда число зубьев колеса Z₂ = Z₁·U = 68. Для косозубых передач по условию отсутствия подрезания Z_min ≥ 17сos³β. Угол наклона линии зуба β принимается для косозубых колёс в пределах β = 8…15°; для шевронных β = 25…40°. В случае дробного передаточного отношения число зубьев колеса округляется до целого, уточняется передаточное отношение и проверяется его отклонение от заданного, не более 2,5%.

Находим все необходимые расчётные коэффициенты.

Коэффициент износа K_изн, учитывающий уменьшение толщины зуба из-за износа по отношению к первоначальной толщине: 10 % − K_изн = 1,25;
20 % − K_изн = 1,5; 30 % − K_изн = 2,00. Полагаем за срок службы износ не более 10 %, тогда K_изн = 1,25.

Выбираем степень точности (табл. 3.9). Передача привода шлагбаума – тихоходная, с пониженными требованиями к точности (фиксированные положения заградительного бруса в крайних положениях допускаются в пределах
± 5°), поэтому будет достаточно выбрать 9-ю степень точности.

По принятой степени точности находим коэффициент динамичности К_FV (табл. 3.7) для прямозубой передачи 9-й степени точности при твёрдости зубьев менее НВ350 и минимальной скорости примем К_FV = 1,3.

Коэффициент концентрации нагрузки К_Fβ, учитывающий неравномерность её распределения по длине зуба, находим, принимая Ψ_bd = 0,4 для симметричного расположения колёс (табл. 3.6) К_Fβ = 1,03.

Коэффициент нагрузки К_F = К_FV ·К_Fβ =1,339.

Коэффициент К_FL, учитывающий неравномерность распределения нагрузки между зубьями, для прямозубых колёс К_FL = 0,7, для косозубых К_FL = 0,8.

Коэффициент ширины венца по модулю Ψ_bm = b/m. Обычно, пропорционально нагруженности передачи, Ψ_bm = 7…15. Для привода шлагбаума, учитывая сравнительно малые нагрузки, предварительно примем Ψ_bm = 7.

Коэффициент наклона зуба Y_β = 1− β/140°. Для прямозубых Y_β = 1.

Коэффициенты прочности зубьев Y_F1 и Y_F2 (табл. 3.8) при отсутствии смещения исходного контура для шестерни Y_F1 = 4,30; для колеса Y_F2 = 3,74.

Для шестерни и колеса находим отношения допускаемых напряжений к коэффициентам прочности: шестерня [σ_F]₁ /Y_F1= 212/4,30 = 49,30; колесо
[σ_F]₂ /Y_F2= 214/3,74 = 57,21. Это отношение меньше у шестерни, поэтому расчёт модуля выполняем, подставляя параметры шестерни: M₁, Z₁,Y_F1.
Вычисляем модуль зацепления по найденным расчётным коэффициентам и параметрам шестерни:

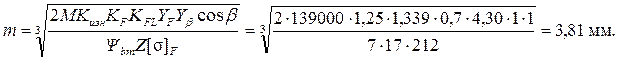
Из нормального ряда модулей (табл. 3.11) выбираем ближайший больший модуль m = 4 мм. В косозубых передачах здесь и далее имеется в виду нормальный модуль m_n.

Находим размеры колёс.

Межосевое расстояние А_W = m · (Z₁ + Z₂) / 2 = 4(17+68)/2 = 170,00 мм.

Делительные диаметры:

d_W1 = m · Z₁ / cosβ = 4 · 17 / 1 = 68 мм;

d_W2 = m · Z₂ / cosβ = 4 · 68 / 1 = 272 мм.

Диаметры вершин:

d_a1 = d_W1 + 2· m = 68 + 2 · 4 = 76 мм;

d_a2 = d_W2 + 2· m = 272 + 2 · 4 = 280 мм.

Диаметры впадин:

d_f1 = d_W1 – 2,5 · m = 68 – 2,5 · 4 = 58 мм;

d_f2 = d_W2 – 2,5 · m = 272 – 2,5 · 4 = 262 мм.

Рабочая ширина зубчатого венца b_W = Ψ_bA· m = 7·4 = 28 мм.

Определяем силы в зацеплении.

Окружная сила: F_t = 2 · М₁ / d_W1 = 2 · 139000 / 68 = 4088 Н.

Радиальная сила: F_r = F_t tg20°/cosβ = 4088 · 0,364 / 1 = 1488 Н.

Осевая сила: F_a = F_t tg β = 4088 · 0 = 0 H (передача прямозубая).

Выполняем проверочный расчёт зубьев на выносливость по напряжениям изгиба. Для этого предварительно находим:

Окружную скорость в зацеплении

V_окр = (π·d_W1·n₁)/(60·1000) = (3,14·68·13,32) /(60000) = 0,047 м/с.

Коэффициент концентрации нагрузки (табл. 3.6)

для Ψ_bd = b_W/d_W1 = 48/68 = 0,7 К_Fβ = 1,065.

Коэффициент нагрузки К_F = К_FV · К_Fβ =1,3·1,065 = 1,385.

С учётом уточнений, напряжения изгиба в опасном сечении зуба колеса:

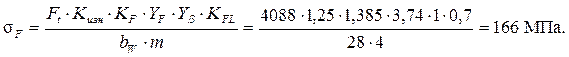
Видим, что напряжения изгиба зуба колеса 166 МПа меньше допускаемых (212 МПа).

Если условие прочности на изгиб не выполняется, то следует повторить расчёт, увеличив модуль m и/или коэффициент ширины венца по модулю
Ψ_bm = b/m.

Однако в нашем случае диаметр вершин ведомого колеса d_a2 = 280 мм не вписывается в заданные для привода габариты (250 мм).

Размеры колеса, а значит и всего привода, можно уменьшить, применив корригированную шестерню с числом зубьев Z₁ = 12. Для этого при нарезании зубьев шестерни необходим коэффициент смещения исходного контура

χ₁ = (17 − Z₁) / 17 = (17 − 12) / 17 = 0,29.

Ведомое колесо не корригируется(χ₂ = 0), что даёт нам неравносмещённое зацепление.

Тогда, для чисел зубьев Z₁ = 12 и Z₂ = Z₁·U = 48 найдём размеры колёс.

Межосевое расстояние:

А_W = m·[(Z₁ + Z₂) / 2 + χ₁]= 4[(12 + 48) / 2 + 0,29] = 121,16 мм.

Диаметры начальных окружностей:

d_W1 = m·Z₁ + 2m·χ₁ =4∙12 + 2∙4·0,29 = 50,32 мм;

d_W2 = m·Z₂ + 2m·χ₂ =4∙48 + 2∙4·0 = 192 мм.

Делительные диаметры, которые после коррекции не совпадают с начальными диаметрами d_W:

d₁ = m · Z₁/ cosβ = 4·12 / 1 = 48 мм;

d₂ = m · Z₂ / cosβ = 4·48 / 1 = 192 мм.

Диаметры вершин:

d_a1 = d₁ + 2 m ·( 1+ χ₁)= 48 + 2·4 ( 1+ 0,29) = 58,32 мм;

d_a2 = d₂ + 2·m = 192 + 2·4 = 200 мм.

Диаметры впадин:

d_f1 = d₁ – 2,5·m + 2·m· χ₁ = 48 – 2,5·4 + 2·4·0,29 = 40,32 мм;

d_f2 = d₂ – 2,5·m = 192 – 2,5·4 = 182 мм.

Силы в зацеплении:

Окружная сила: F_t = 2 · М₁ / d_W1 = 2·139000/50,32 = 5524 Н.

Радиальная сила: F_r = F_t tg20°/cosβ = 5524·0,364/1 = 2010 Н.

Осевая сила: F_a = F_t tg β = 5524·0 = 0 H (передача прямозубая).

В рассчитанной корригированной передаче (Z₁ =12) с модулем m = 4, напряжения изгиба в опасном сечении зуба колеса составят:

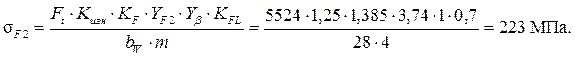
Изгибные напряжения больше допускаемых (212 МПа), поскольку увеличилась окружная сила. Компенсируем это увеличением рабочей ширины зубчатого венца до b_W = 32 мм. Тогда изгибные напряжения зуба колеса:

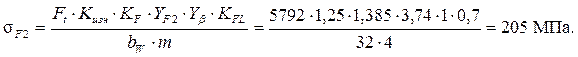
Теперь условие изгибной прочности выполняется (205 МПа < 212 МПа).

Производим проверочный расчет контактных напряжений на рабочих поверхностях зубьев. В общем случае формула записывается в виде:

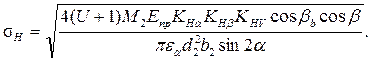
Окружная скорость на делительном диаметре колес:

V_max = (π ·d_W1·n₁)/60 000 = (3,14 · 48 ·13,32) /60 000 = 0,033 м/с.

Для такой малой скорости назначаем 9-ю степень точности (табл. 3.9), применяемую для тихоходных передач с пониженными требованиями к точности.

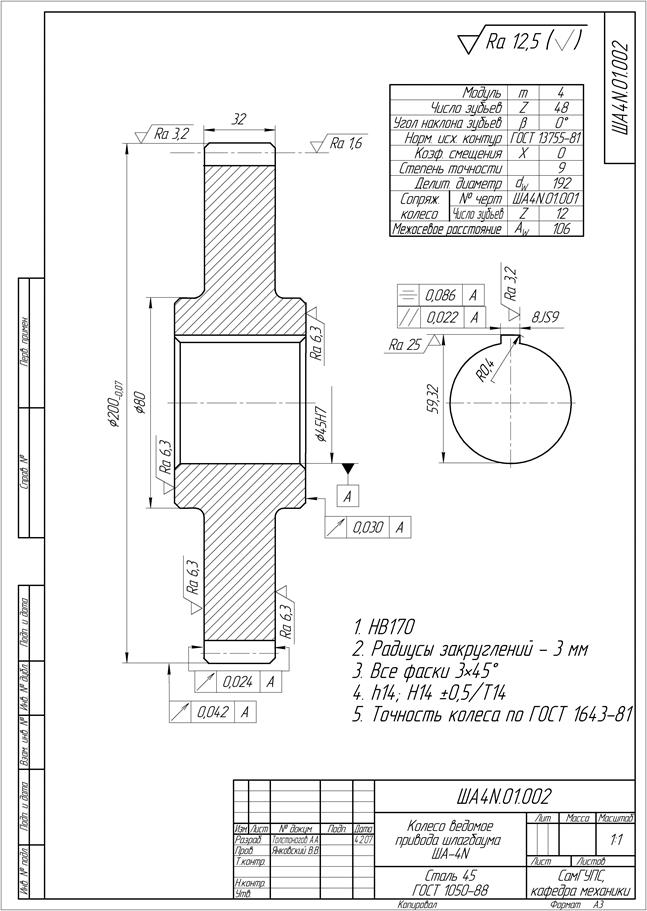
Рис. 3.9 Рабочий чертёж цилиндрического зубчатого колеса

Выбираем коэффициенты (табл. 3.2...3.7) распределения нагрузки К_Hα=1, концентрации нагрузки (для b_W = 32 мм и d_W1 = 48 мм; Ψ_bd = b_W/d_W1 = 0,667; симметричное расположение колёс) K_Hβ = 1,025; динамичности приложения нагрузки K_HV = 1,04. β_b – угол наклона линии зуба к образующей основного цилиндра β_b = arcsin(sinβ·cosα) =arcsin(sin0°·cos20°) = 0°; ε_α =1,05…1,1 – коэффициент перекрытия, примем ε_α =1,07;

С учётом всех коэффициентов контактные напряжения в зубьях колеса

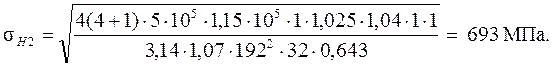
Контактные напряжения меньше допускаемых (703 МПа). Условие контактной прочности выполнено.

Шестерня корригированная, Z₁ =12; m = 4; χ₁ = 0,29; β = 0; d_W1 = 48 мм;
d_a1 = 58,32 мм; d_f1 = 40,32 мм; b_W = 32 мм.

Колесо некорригированное, Z₂ = 48; m = 4; β = 0; d_W2 = 192 мм;
d_a2 = 200 мм; d_f2 = 182 мм; b_W = 32 мм.

По результатам расчёта выполняются рабочие чертежи (рис. 3.9).

3.5. Расчёт планетарной передачи. Привод шуруповёрта ШВ-2М

Планетарные передачи применяются в качестве распределительных механизмов, позволяя регулировать потоки мощности путём торможения различных звеньев и как дифференциальный механизм. Эти передачи компактны и имеют малую массу. Симметричное расположение сателлитов снижает нагрузки на валы и замыкает силы внутри передачи. Всё это обеспечивает снижение вибрации, шума и потерь на трение.

Наибольшее распространение получили планетарные передачи, в которых, с целью выравнивания нагрузки по потокам, одно из центральных колес выполняют самоустанавливающимся (плавающим).

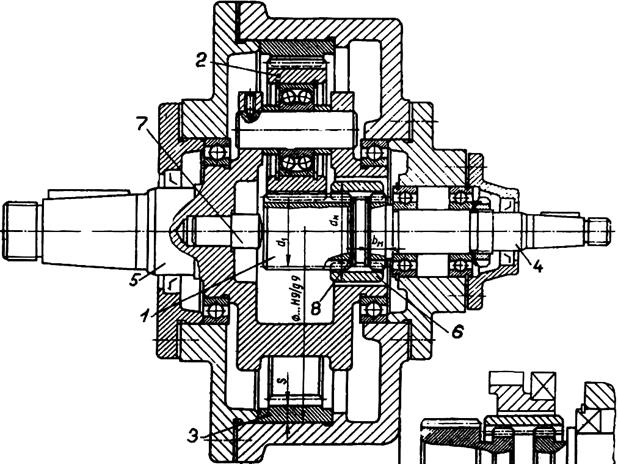
В планетарном редукторе с плавающим солнеч­ным колесом ведущий вал 4 посредством зубчатой муфты 6 соединён с солнеч­ным колесом 1. Солнечное колесо ограничено от осевого смещения подпятником 7 и кольцом 8.

Планетарные редукторы с плавающим корончатым колесом сложнее по конструкции и поэтому не нашли широкого применения (рис. 3.10).

Конструкция планетарного редуктора в значительной степени определяется техническим заданием, и поэтому ниже будут рассмотрены варианты выполнения основных деталей и узлов редуктора применительно к его различным исполнениям.

Ведущий быстроходный вал изготавливают из конструкционной стали с последующей термообработкой зубчатого венца до твердости HRC45…50.

Рис. 3.10. Планетарный редуктор с плавающим солнечным колесом

Известны три варианта исполнения установки вала на опорах ка­чения.

Если на входном конце вала установлена соединительная муфта, то необходимо применять вариант а (рис. 3.11), а усилие F от неравномерности распределения общего момента по потокам следует принять по формуле:

F = 0,4·M₁/d₁, где d₁ − делительный диаметр зубьев зубчатой муфты.

Консольная нагрузка F_K зависит от конструкции муфты и величины смещения валов. Для наиболее распространённой упругой втулочно-пальцевой муфты (МУВП) F_K можно определить по формуле: F_K = Δ · С,

где Δ − радиальное смещение валов, С − радиальная жесткость, принимаемая в зависимости от диаметра вала d:

Подшипники принимают при компоновке предварительно легкой серии. Если на ведущем быстроходном валу установлен шкив ременной передачи или звездочка цепной, то необходимо применять конструкцию по схеме б (рис 3.11), где правый подшипник принимается средней серии, а величину F_K определять по нагрузкам от ременной и цепной передач.

Конструкция ведущего вала по схеме в (рис 3.11) применяется в мотоp-редуктоpах.

Конструкция ведомого вала и водила зависит от серийности производства. При массовом и серийном производствах применяют ведомый вал из высокопрочного чугуна ВЧ50-2 или ВЧ60-2, отлитый совместно с водилом.

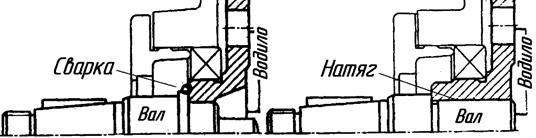
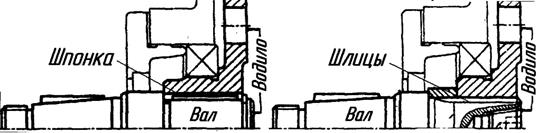
При единичном и мелкосерийном производстве вал и водило изготав­ливают из стали отдельно и соединяют сваркой, посадкой с натягом, шпонками либо шлицами.

Рис. 3.12. Варианты соединения вала с водилом

Водило конструируют в основном с одной стенкой, в которой оси сателлитов располагаются консольно.

Нагрузка от неравномерного распределения потоков определяется по формуле F = 0,2 M / A_W, где M − момент на выходном (ведомом) валу,
A_W − межосевое расстояние, F_К − нагрузка выходного конца вала, рассчитываемая аналогично ве­дущему быстроходному валу.

Учитывая идентичность нагрузок ведущего и ведомых валов, подшип­ники применяются тех же серий и рассчитываются те, которые наиболее нагружены.

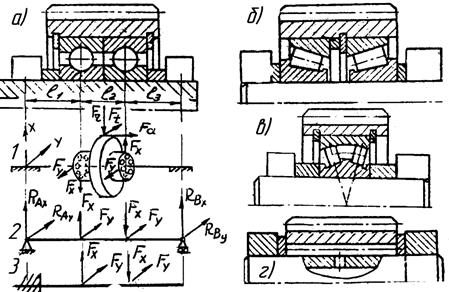
Самыми нагруженными в планетарном редукторе оказываются опоры сателлитов. Существуют различные варианты исполнения опор сателлитов на подшипниках качения, им соответствуют различны схемы нагружения.

Схема нагружения (рис. 3.13, а) используется для определения нагрузок подшипников. Схемы нагружения (рис. 3.13, б,в) предназначены для расчета осей сателлитов, устанавливаемых на водиле соответственно с двумя и од­ной стенками. Величины l₁, l₂, и l₃ определяют при компоновке редуктора. Варианты выполнения конструкции (рис. 3.13, а,б) можно применять как для прямозубых, так и для косозубых передач.

Вариант со сферическим подшипником (рис. 3.13, в) применяется только для прямозубых передач. В случае малых габаритов сателлита необходи­мо использовать вариант с игольчатыми подшипниками (рис. 3.13, г).

В предварительных расчетах при компоновке принимают подшипники средней серии.

С целью обеспечения прочности муфты, соединяющей солнечное коле­со и ведущей вал, принимаем её диаметр d_m ≥ d₁ + 6m, толщину неподвижного колеса S ≥ 2,5m + 2, толщину обода сателлитов S ≥ 2m + 1.

Рис. 3.13. Варианты выполнения опор сателлитов

Корпус редуктора обычно выполняют из чугуна марки СЧ-15, СЧ-2О, а иногда, с целью облегчения, алюминий марок АЛ-2, АЛ-3.

Смазка узлов трения планетарных передач при скорости сателлитов

V_C = 0,5·W_h·d₂ < 5 м/с

производится окунанием с объемом масляной ванны 0,5 л на 1 кВт передаваемой мощности и глубиной погружения сателлитов не менее высоты зубьев.

При V_C > 5 м/с применяют циркуляционную систему смазки.

При окружной скорости колес, окунающихся в ванну V_C ≥ 3 м/с под­шипники смазываются за счет масляного тумана и брызг, при V_C ≤ 3 м/с рекомендуется применять пластичные смазки.

Методику расчёта планетарной передачи покажем на примере редуктора шуруповёрта ШВ2М, применяемого для завёртывания и отвёртывания гаек клеммных и закладных болтов шурупов, а также сверления отверстий под шурупы и костыли в деревянных шпалах (рис. 3.14).

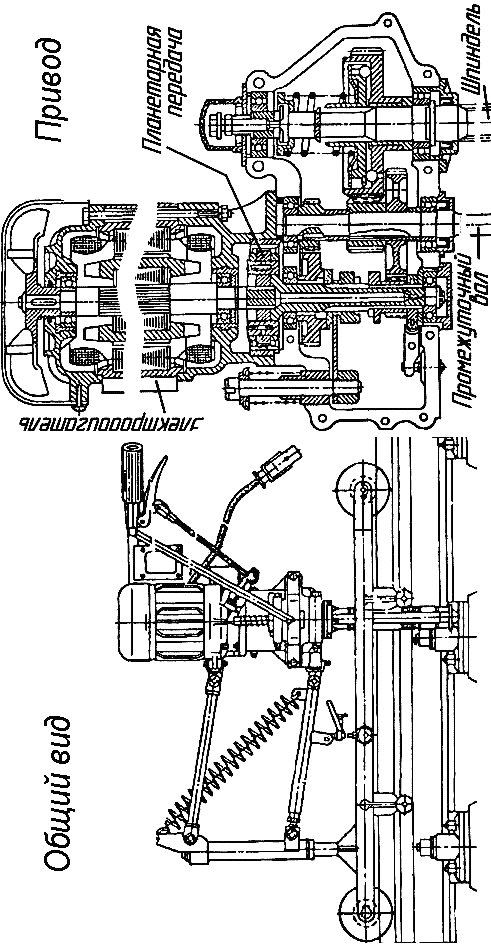
Рис. 3.14. Привод ШВ2М с планетарным редуктором

Вращающий момент от двигателя поступает на планетарную передачу, после которой на коробку передач, где может переключаться либо на шпиндель сверла (промежуточный вал), либо на шпиндель головки шуруповёрта/гайковёрта (выходной вал).

Планетарная передача на первой ступени редуктора применена с целью разгрузки органов управления за счёт замыкания сил в механизме. Кроме того, для сверления отверстий и завинчивания/отвинчивания необходима возможность регулирования частоты вращения и вращающего момента, что тоже характерно для планетарных передач.

Рассмотрим рабочие параметры шуруповёрта с целью формирования исходных данных для расчёта планетарной передачи.

Шуруповёрт приводится трёхфазным асинхронным двигателем мощностью N_дв = N₁ = 1700 Вт с частотой вращения n_дв = n₁ = 2800 об/мин. При этом на валу развивается вращающий момент M₁ = N₁·30/(n₁·π) =5,8 Нм.

Наиболее тяжёлый режим работы – отвинчивание болтов, гаек и шурупов при разборке старых путей. При этом для обеспечения паспортных параметров на шпинделе шуруповёрта (M_шп = 900 Нм, n_шп = 45 об/мин) вращающий момент, передаваемый на коробку передач, должен быть равен M₂ = 30 Нм.

Шуруповёрт должен обеспечить ресурс 600 часов работы.

Кроме того, габариты планетарной передачи не должны превышать120 мм. Это значит, что диаметр впадин корончатого колеса (d_f3) не должен быть более 100 мм.

Определим параметры на ведомом (выходном) валу планетарной передачи.

КПД передачи примем η = 0,96. Тогда мощность на выходном валу (водиле) N₂ = N₁·η = 1700·0,95 = 1620 Вт.

С учётом требуемого выходного вращающего момента найдём угловую скорость на выходном валу передачи ω₂ = N₂/M₂ = 1620/30 = 54,0 с⁻¹. Частота вращения водила n₂ = 30ω₂/π = 30·54,0/3,14 = 516 об/мин.

Передаточное отношение проектируемой планетарной передачи
U = n₁ / n₂ = 2800 / 516 = 5,43. Передача с таким передаточным отношением будет нестандартной.

Ресурс 600 часов означает число циклов (оборотов) ведущего вала
N_HE1 = 600·60·2800 = 1,008·10⁸ циклов. Число циклов (оборотов) выходного вала водила с учётом передаточного отношения планетарной передачи
N_HE2 = N_HE1/ U = 1,008·10⁸/5,43 = 1,856·10⁷ циклов.

По этим исходным данным рассчитываем планетарную передачу [47].

В соответствии с принятым передаточным отношением выбираем кинематическую схему планетарной передачи.

Учитывая требуемое передаточное отношение, принимаем наиболее распространённую схему с неподвижным корончатым колесом (рис. 3.15, а), обозначаемую 2K−h.

Если 1,8 < U < 2,8, то необходимо изменить число оборотов ведущего вала n₁.

Для разделения передаваемой мощности на несколько потоков в планетарной передаче применяются несколько сателлитов, не менее двух для уравновешивания нагрузок на подшипники водила. Благодаря такой многопоточности передаваемой мощности уменьшаются масса и габариты планетарных передач. Сателлиты размещаются по окружности равномерно. Оптимальное число сателлитов 3, но в нашем случае, учитывая малые габариты передачи, для упрощения конструкции водила принимаем минимальное число сателлитов N_C = 2.

Выбираем минимальное число зубьев солнечного колеса Z₁ = 17.

Определяем число зубьев сателлита: Z₂ = Z₁(U−2)/2 = 17·(5,43−2)/2 =
= 29,155. Округляем Z₂ до 30.

Определяем число зубьев корончатого колеса из условия соосности:

Z₃ = Z₁ + 2 ·Z₂ = 17+2 ·30 = 77.

Проверяем условие сборки: (Z₃− Z₁)/N_С(должно быть целое)

(Z₃− Z₁)/N_C = (77−17)/2 = 30. Условие выполняется.

При невыполнении условий из­меняется либо число сателлитов, либо число зубьев солнечного колеса.

Проверяем условие соседства: (Z₁+Z₂)sin(3,14/N_C) − (Z₂+2) > 0.

(17+30)·sin(3,14/2) − (30+2) = 47−32 = 15 > 0. Условие выполняется.

При невыполнении условий из­меняется либо число сателлитов, либо число зубьев солнечного колеса.

Далее расчет выполняем, как для обычной цилиндрической переда­чи с внешним зацеплением. В передачах, где сателлит входит в заце­пление с двумя центральными колесами (солнечным и корончатым), а механические свойства примерно одинаковы, на прочность рассчитыва­ется только внешнее зацепление (солнечное колесо − сателлит). Если материалы колес различны, то дополнительно выполняется прове­рочный расчет внутреннего зацепления (сателлит – корончатое колесо) [52].

Вращающий момент на колесе (сателлите) равен:

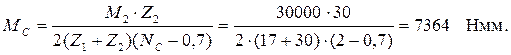
Частоту вращения солнечного колеса при неподвижном водиле найдем по формуле n_H0 = n₁−n_н = 2800 − 516 = 2284 об/мин; число оборотов сателлита
n_С = n_H0·Z₁/Z₂ = 2284·17/30 = 1294 об/мин.

Выбираем материал (табл. 3.1) шестерни и колеса (солнечного колеса и сателлита) с условием, что твердость колеса ниже твер­дости шестерни на 30…40 единиц HB. В дальнейшем при расчетах будем считать солнечное колесо шестерней, а сателлит − колесом.

Шестерня: сталь 45 улучшенная, HB265, Е = 2,1·10⁵ МПа,

σ_Hlim =1,8НВ+65 = 542 МПа, S_H = 1,1; σ_Flim = 1,8НВ = 477 МПа, S_F =1,65.

Колесо: сталь 45 нормализованная, HB217, Е = 2,1·10⁵ МПа,

σ_Hlim =1,8НВ+ 65 = 455 Мпа; S_H=1,1; σ_Flim = 1,8НВ = 390 МПа, S_F = 1,65.

Определяем базовое число циклов нагружения:

для шестерни N_H01 = 30·235^2,4 = 1,47·10⁷ циклов;

для колеса N_H02 = 30·200^2.4 = 9,9·10⁶ циклов;

для стального колеса и шестерни N_F0 = 4·10⁶.

Фактическое число циклов нагружения определено с учётом частоты вращения по заданному ресурсу шуруповёрта: для шестерни N_HE1 = 1,008·10⁸ циклов; для колеса N_HE2 = 1,856·10⁷ циклов.

Коэффициенты долговечности вычисляются так же, как у всех зубчатых передач (разд. 3.2) по контактным напряжениям, а поскольку в нашем случае N_HE > N_H0, коэффициент K_HL = 1. По изгибным напряжениям для выбранных материалов K_FL1 = (N_F01/N_FE1)^1/6= (4·10⁶/1,008·10⁸)^0,16 = 0,584; примем K_FL1=1;

K_FL2 = (N_F02/N_FE2)^1/6 = (4·10⁶/2,016·10⁸)^0,16 = 0,521; примем K_FL2=1.

Реверс шуруповёрта осуществляется переключением зубчатых колёс на второй ступени, а планетарная передача − нереверсивная, поэтому K_FC =1.

Допускаемые контактные напряжения [σ_H] = (σ_Hlim/S_H)·K_HL:

для шестерни [σ_H]₁ = (542/1,1) ·1 = 492 МПа;

для колеса [σ_H]₂ = (455/1,1) ·1 = 414 МПа.

Принимаем в расчёт минимальное [σ_H] = 414 МПа.

Определяем минимальное межосевое расстояние из условия контакт­ной прочности

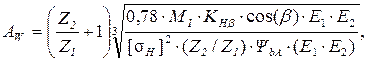
где K_Hβ − коэффициент концентрации переменной нагрузки (табл. 3.3) принимаем при твёрдости < НВ350 и несимметричном расположении колес
K_Hβ = 1,2.

Коэффициент ширины венца Ψ_bA:

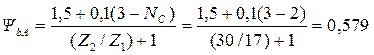
принимаем из стандартного ряда (табл. 3.10) Ψ_bA = 0,63;

β − угол наклона зубьев, для прямозубой передачи β = 0°.

С учётом принятых коэффициентов межосевое расстояние равно:

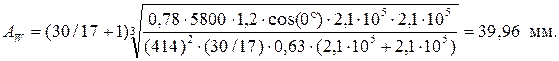
Определяем нормальный модуль передачи

m = 2·A_W·cos(β)/(Z₁+Z₂) = 2·39,96·1/(17+30) = 1,70 мм,

полученный модуль округляем до стандартного m =1,75 мм.

Уточняем межосевое расстояние передачи

A_W = 0,5·(Z₁+Z₂) ·m/cos(β) = 0,5·(17+30) ·1,75/cos(0°) = 41,13 мм, полученное значение округляем до ближайшего целого A_W = 41 мм.

Уточняем угол наклона линии зуба для косозубых передач

β = arccos[0,5(Z₁+Z₂)·m/A_W].

Рассчитываем геометрические параметры зубчатой передачи.

Делительный диаметр:

− шестерни (солнечного колеса) d_W1 = m·Z₁/cos(β) = 1,75·17/1 = 29,75 мм;

− колеса (сателлита) d_W2 = m·Z₂/cos(β) = 1,75·30/1 = 52,5 мм;

− корончатого колеса d_W3 = m·Z₃/cos(β) = 1,75·77/1 = 134,75 мм > 100 мм.

Здесь мы видим, что конструктивное ограничение габарита передачи
(d_W3 < 100 мм) не выполняется.

Необходимо корректировать параметры и проводить повторный расчёт.

Для уменьшения межосевого расстояния A_W необходимы другие материалы колёс с более высокими допускаемыми напряжениями. Примем для всех колёс (табл. 3.1) сталь 45ХН НВ540, поверхностная закалка HRC55;
Е = 2,1·10⁵ МПа, σ_Hlim = 1020 Мпа, S_H = 1,1; σ_Flim = 550 МПа, S_F =1,7.

Допускаемые контактные напряжения для закалённой стали 45ХН

[σ_H] = (σ_Hlim /S_H)·K_HL= (1020/1,1) ·1 = 927 МПа.

Уменьшим также число зубьев солнечного колеса до Z₁ = 14.

Тогда новое число зубьев сателлита: Z₂ = 14·(5,43−2)/2 = 24,01 ≈ 24.

Число зубьев корончатого колеса: Z₃ = Z₁ + 2 ·Z₂ = 14 + 2 ·24 = 62.

Условие сборки: (Z₁+Z₃)/N_C = (14+62)/2 = 38, целое. Выполняется.

Условие соседства: (Z₁+Z₂)sin(3,14/N_C) − (Z₂+2) = (14+25)·sin(3,14/2) −
– (24+2) = 13 > 0 также выполняется.

Вращающий момент на колесе (сателлите) равен:

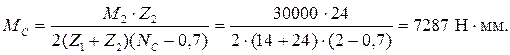
Межосевое расстояние для закалённых колёс после корректировки всех расчётных параметров

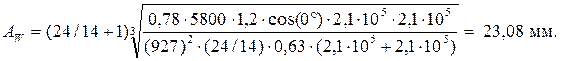
Нормальный модуль передачи с закалёнными колёсами

m = 2 · A