Привод системы охлаждения генератора тепловоза 2ТЭ10Л
Конические зубчатые передачи выходят из строя по тем же причинам, что и цилиндрические. Поэтому и рассчитываются они аналогично, лишь с использование параметров эквивалентных цилиндрических передач.
При этом из опыта эксплуатации известно, что из-за существенного влияния на работу неточностей взаимного расположения колёс, конические передачи могут передавать нагрузку не более 85 % от эквивалентных цилиндрических.
Конические прямозубые колёса применяют при окружных скоростях до
2 м/с. При более высоких скоростях применяются колёса с круговыми зубьями, которые дают более плавное зацепление и несущую способность в 1,45 раза выше, чем у прямозубых при тех же размерах. Колёса с круговыми зубьями менее чувствительны к нарушению точности взаимного расположения колёс.
Основные размеры конических колёс определяют с корректирующим коэффициентом ν(H,F), который зависит от вида колёс (прямозубые или с круговыми зубьями) и вида нагружения (изгибные или контактные напряжения).
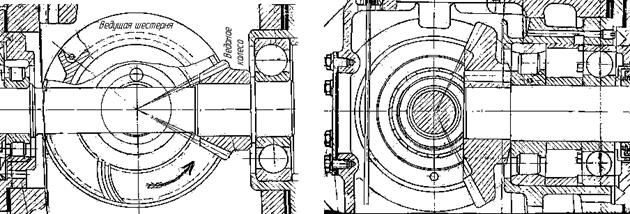
Расчёт конической передачи покажем на примере мультипликатора привода вентилятора системы охлаждения генератора тепловоза 2ТЭ10Л (рис. 3.24).
Отбираемая от двигателя мощность N1 = 25 Л.С. = 18,4 кВт. Частота вращения вала отбора мощности n1 = 850 об/мин. В то же время для привода вентилятора необходима частота вращения n2 = 1880 об/мин.
|
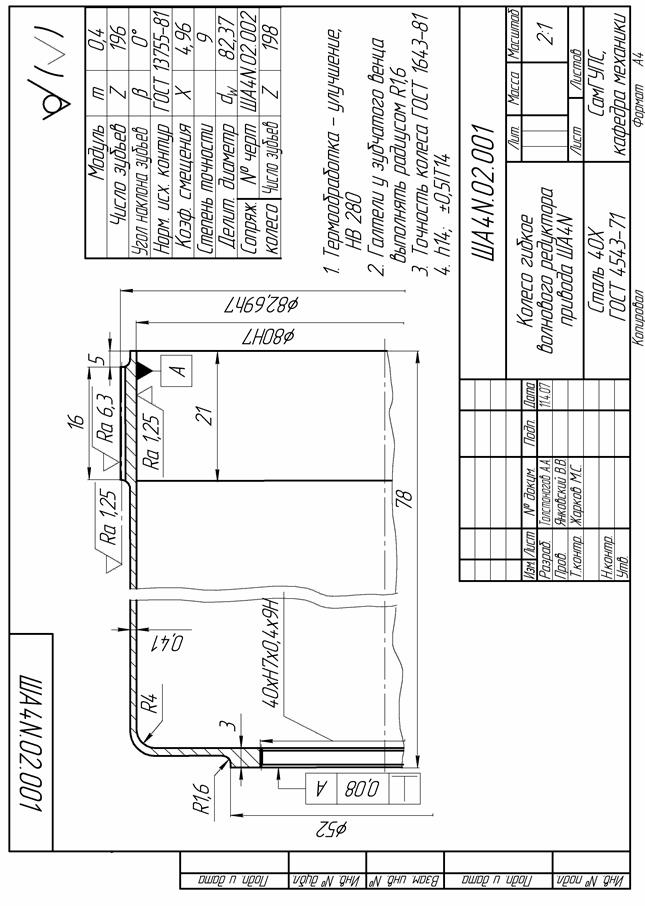
| Рис. 3.23. Рабочий чертёж гибкого зубчатого колеса |
Это значит, что передача должна быть повышающей, а передаточное отношение жёстко задано режимом работы привода U = n1/n2 = 850/1800 =
= 0,472. Этого значения не предусмотрено в нормальном ряду. Такая передача является нестандартной.
|
| Рис. 3.24. Мультипликатор привода вентилятора 2ТЭ10Л, фрагмент |
Как всегда и везде, обозначим индексом 1 и будем называть шестерней ведущее колесо, а индексом 2 – ведомое. В нашем случае передача повышающая и передаточное отношение меньше 1, а это значит, что шестерня будет больше колеса.
Кроме того, следует иметь в виду, что все расчётные формулы обычно приводятся для понижающих передач. А в случае повышающей передачи в расчётные формулы вместо передаточного отношения U следует подставлять обратную величину 1/U.
Вращающий момент на ведущем валу M1 = 30·N1/(π·n1) =
= 30·18400/(3,14·850) = 207 Нм. КПД конической передачи примем η = 0,95.
На ведомый вал придёт мощность, передаваемая вентилятору N2 = N1·η =
= 18400·0,95 = 17480 Вт. Вращающий момент на ведомом валу
M2 = 30·N2/(π· n2) = 30·17480/(3,14·1800) = 93 Нм.
Ресурс работы мультипликатора назначен Lр = 109 оборотов, что соответствует паспортному пробегу локомотива порядка 1 млн. км при среднерасчётной скорости 55 км/час. Это значит, что мы должны спроектировать коническую передачу на ресурс ведущего вала (шестерни) NFE1 = NНE1 =109 циклов и ведомого вала (колеса) на ресурс NFE2= NFE1·U. Подставляем для повышающей передачи (1/U) NFE2= 109·(1/0,472) = 2,118·109 циклов.
Этих исходных данных достаточно, чтобы начинать расчёт [43].
Выбираем материалы колёс.
Рекомендуется выбирать материалы и назначать термообработку таким образом, чтобы твёрдость поверхности зубьев меньшего колеса (здесь − ведомое) была выше, чем у большего (здесь – ведущее).
Охлаждение локомотивного двигателя – крайне ответственная система, выход из строя которой повлечёт за собой поломку двигателя. Поэтому выбираем материалы (табл. 3.1):
− для ведущей шестерни сталь 40Х, термообработка – закалка объёмная НВ425, HRC40, модуль упругости E1 = 2,1·105 МПа, предел контактной выносливости σНlim1 = 18,5HRC+135 = 18,5∙40 + 135 = 875 МПа, коэффициент контактной безопасности SН1 = 1,2 МПа; предел изгибной выносливости
σFlim1 = 600 МПа; коэффициент изгибной безопасности SF1 = 1,7;
− для ведомого колеса сталь 40Х, с поверхностной закалкой НВ600, HRC60, модуль упругости E2 = 2,1·105 МПа, предел контактной выносливости σНlim2 = = 1005 МПа; коэффициент контактной безопасности SН1 = 1,2 МПа; предел изгибной выносливости σFlim2 = 650 МПа; коэффициент изгибной безопасности SF1 = 1,7.
Передача нереверсивная, коэффициент KFC =1.
Базовые числа циклов контактных напряженийNHO:
для шестерни NНО1 = 30НВ2,4 = 30·4252,4 = 0,6·108;
для колеса NНО2 = 30·6002,4 = 1,39·108.
Базовое число циклов изгибных напряжений NFO1 = NFO2 = 4·106.
Рассчитаем коэффициенты долговечности (см. разд. 3.2):
KHL1 = (NHO1/NHE1)1/20 = (0,6·108/109)1/20 = 0,869;
KHL2 = (NHO2/NHE2)1/20 = (1,39·108/2,118∙109)1/20 = 0,872;
KFL1 = (NFO1/NFE1)1/6 = (4·106/109)1/6 = 0,398; примем 1;
KFL2 = (NFO2/NFE2)1/9 = (4·106/2,118·109)1/9 = 0,498; примем 1.
Вычисляем допускаемые контактные напряжения:
[σН]1 = (σНlim1 /SH1)·KHL1 = (875/1,2)·0,869 = 633 МПа;
[σН]2 = (σНlim2 /SH2)·KHL2 = (1005/1,2)·0,872 = 730 МПа.
Вычисляем допускаемые напряжения при изгибе:
[σF]1 = (σFlim1 /SF1)·KFC1·KFL1 = (600/1,7)·1·1 = 353 МПа;
[σF]2 = (σFlim2 /SF2)·KFC2·KFL2 = (650/1,7)·1·1 = 382 МПа.
Определяем числа зубьев и передаточное число. Если они не заданы, то число зубьев меньшего колеса принимают не менее 17, а число зубьев большего колеса – для понижающей передачи ближайшее целое к 17·U (или 17/U, если передача повышающая). Для нашей передачи принимаем Z2 =17, Z1 = Z2/U = 17/0,472 = 36,01 ≈ 36. Уточняем фактическое передаточное отношение Uфакт = Z2/Z1 = 17/36 = 0,4722 и проверяем его отклонение от заданного,
δ = (Uфакт − U)/U = (0,4722 −0,472)/0,472 = 0,04 %. Это расхождение допустимо, поскольку не превышает 2,5 %. В дальнейших расчётах подставляем U = Uфакт.
Определяем внешний делительный диаметр шестерни
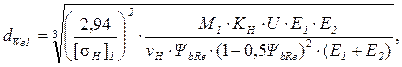
где KH – коэффициент нагрузки, учитывающий дополнительные вредные нагрузки, сопутствующие работе передачи. При проектном расчете предварительно принимают KH = 1,2 для колес с твердостью поверхностей зубьев
≤ HB350 (как в нашем случае) и KH = 1,35 при твердости > HB350;
ΨbRе – коэффициент ширины зубчатого венца ΨbRе = b/Re ≤0,3, при выполнении проектного расчета рекомендуется принимать ΨbRе= 0,285;
νН – корректирующий коэффициент, который для прямых зубьев равен 0,85, а для круговых находится по формулам в зависимости от твёрдости материала и передаточного отношения:
| HB1 ≤ 350; HB2 ≤ 350 | HRC1 ≥ 45; HB2 ≤ 350 | HRC1 ≥ 45; HRC2 ≥ 45 |
| νН =1,22+0,21U | νН =1,13+0,13 U | νН =0,81+0,15 U |
Для нашего случая (HRC1 = 40; HRC2 = 60):
νН = 0,81+0,15·(1/U)= 0,81+0,15·(1/0,472) = 1,12.
Внешний делительный диаметр шестерни нашей передачи:
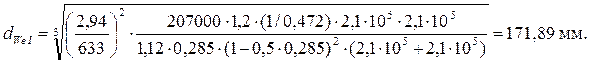
Стандартный ряд значений внешнего делительного диаметра колеса, мм по ГОСТ 12289−76: 50, 56, 63, 71, 80, 100, 112, 125, 140, 160, 180, 200, 225, 250, 280, 315, 355, 400, 450, 500. Принимаем dWе1 = 180 мм.
Рассчитываем геометрические параметры колёс (ГОСТ 19326-73):
− внешний окружной модуль me= dWe1/Z1=180/36 = 5 мм;
− углы делительных конусов шестерни и колеса:
δ1 = arctgU = arctg(1/0,472) = 64°43'12'', δ2 = 90° − δ1 = 25°16'48'';
− внешний делительный диаметр колеса dWe2=me·Z2 = 5·17 = 85 мм;
− внешнее конусное расстояние
Re = 0,5de1/sinδ1 = 0,5·180/sin(64°43'12'') = 99,55 мм;
− ширина зубчатого венца (минимальная)
для стандартных передач b =ΨbRе·Re;
для нестандартных передач
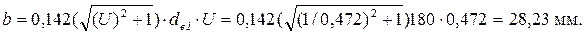
Принимаем ширину венца b = 30 мм.
− среднее конусное расстояние R = Re− 0,5b = 99,55 − 0,5·30 = 84,55 мм;
− средний окружной модуль m = me∙R/Re = 5·84,55 / 99,55= 4,246 мм;
− средние делительные диаметры:
шестерни dW1 = m∙Z1 = 4,246·36 = 152,88 мм;
колеса dW2 = m∙Z2 = 4,246·17 = 72,18 мм;
− внешняя высота зуба hе= 2,2 me = 2,2·5 = 11 мм;
− внешняя высота головки зуба haе= me = 5 мм;
− внешняя высота ножки зуба hƒе=1,2me =1,2·5 = 6 мм;
− угол ножки зуба θƒ = arctg(hƒе/Re) = arctg (6/81,38) = 4°12'36'';
− угол головки зуба θα = θƒ = 4°12'36'';
− внешний диаметр вершин:
для прямозубых dae1= de1 + 2mecos δ1; dae2= de2 + 2mecos δ2;
для круговых зубьев
dae1= de1 + 1,64mecos δ1= 180+1,64·5·cos(64°43'12'') = 183,50 мм;
dae2= de2 + 1,64mecos δ2 = 85+1,64·5·cos(25°16'48'') = 92,42 мм.
Проводим проверочный расчёт контактных напряжений на рабочих поверхностях зубьев шестерни:
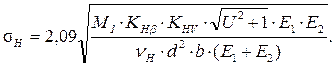
Здесь KHβ − коэффициент концентрации нагрузки, учитывающий распределение нагрузки по ширине венца (табл. 3.3), для консольной шестерни, где Ψbd=30/152,88 ≈ 0,20 находим КНβ = 1,15.
Для окружной скорости V = πdW1n1/60000 = 3,14·152,88·850/60000 =
= 6,80 м/с можно рекомендовать (табл. 3.9) 7-ю степень точности, характерную для передач с повышенными скоростями при умеренных нагрузках.
КНV − коэффициент, учитывающий влияние динамической нагрузки в зацеплении (табл. 3.4), для 7-й степени точности и скорости V = 6,80 м/с выбираем КНV = 1,10.
С учётом выбранных коэффициентов контактные напряжения равны:
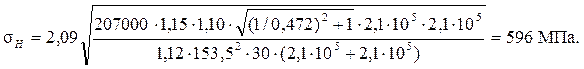
Эти напряжения меньше допускаемых (633 МПа). Условие контактной прочности выполняется.
Если напряжения окажутся больше допускаемых, то можно выбрать другие материалы, которые дали бы повышенные допускаемые напряжения при тех же размерах колёс. Однако, если превышение контактных напряжений над допускаемыми невелико, такой путь приведёт к большим запасам по прочности и неоправданному удорожанию колёс. В этом случае лучше увеличить внешний делительный диаметр колеса, а соответственно и модуль, хотя это и приведёт к некоторому увеличению размеров колёс.
Определяем силы в зацеплении:
− окружная сила определяется одинаково при любом виде зубьев
Ft = 2M1 /dW1 = 2·207000/152,9 = 2707 H;
− осевая сила на колесе, равная радиальной силе на шестерне:
для прямозубых (α = 20°) Fa2= Fr1= Ft·tgα·sinδ2;
для круговых зубьев Fa2 = Fr1 = Ft·(0,44sinδ2 + 0,7cosδ2) =
= 2707(0,44sin25°16'48'' + 0,7 cos25°16'48'') = 2220 Н;
− радиальная сила на колесе, равная осевой силе на шестерне:
для прямозубых (α = 20°) Fr2 = Fa1 = Ft·tgα·cosδ2
для круговых зубьев Fr2 = Fa1 = Ft ·(0,44 cosδ2− 0,7 sinδ2) =
= 2697(0,44 cos25°16'48''+ 0,7 sin25°16'48'') = 271 H.
Выполняем проверочный расчёт на выносливость по напряжениям изгиба. При этом коэффициент прочности зуба находят:
– для прямозубых колёс по эквивалентным числам зубьев ZV1(2) = Z1(2)/cos δ1(2);
– для круговых по биэквивалентному числу зубьев [52]
ZV1 = Z1/(0,55∙cosδ1) = 36/(0,55∙cos 64°43'12'') = 153,4;
ZV2 = Z2/(0,55∙cosδ2) = 17/(0,55∙cos 25°16'48'') = 34,2.
Для ZV1 = 83 и ZV2 = 19 по таблице 3.8 принимаем YF1 = 3,60; YF2 = 3,76.
|
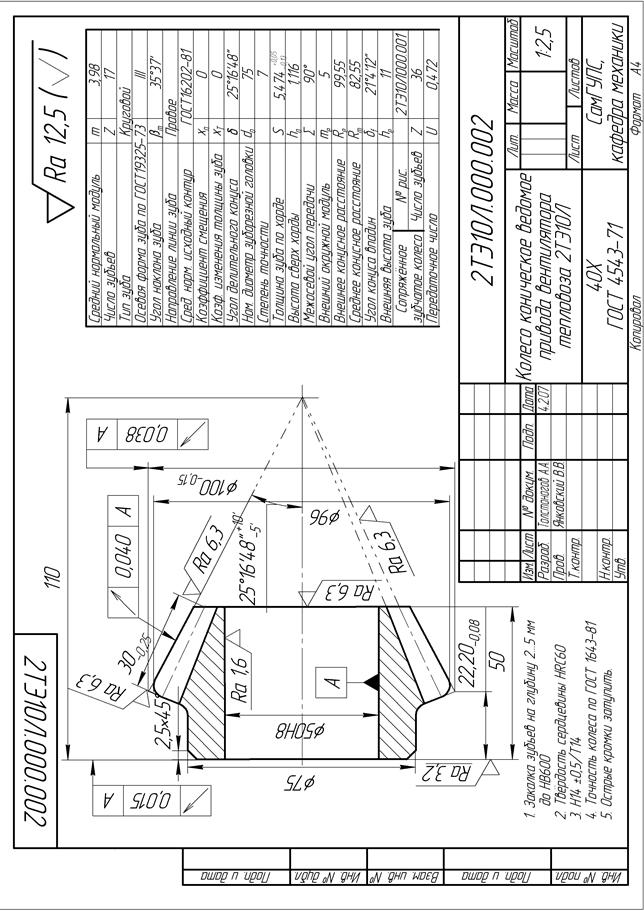
| Рис. 3.25. Рабочий чертёж конической зубчатой шестерни |
Для шестерни и колеса находим отношения допускаемых напряжений к коэффициентам прочности: шестерня [σF]1/YF1= 353/3,60 = 98,05; колесо [σF]2 /YF2 = 190/3,76 = 50,53. Это отношение меньше у колеса, поэтому расчёт модуля выполняем, подставляя параметры колеса: M2, Z2,YF2.
Коэффициент динамичности КFV, учитывающий динамическое действие нагрузки для 7-й степени точности и окружной скорости колеса V = 6,80 м/с принимаем (табл. 3.7) КFV = 1,25.
Коэффициент КFβ , учитывающий неравномерность распределения нагрузки по длине зуба, для консольного колеса на шариковом и роликовом подшипниках с коэффициентом ширины венца Ψbd = 30/72,8 ≈ 0,4 примем (табл. 3.6) КFβ ≈ 1,6.
Корректирующий коэффициент νF для прямозубых колёс равен 0,85, а для круговых зубьев находится по формуле в зависимости от твёрдости зубьев и передаточного отношения U:
| HB1 ≤ 350; HB2 ≤ 350 | HRC1 ≥ 45; HB2 ≤ 350 | HRC1 ≥ 45; HRC2 ≥ 45 |
| νF = 0,94+0,08 U | νF = 0,85+0,043 U | νF = 0,65+0,11 U |
Для HRC1 = 45; HRC2 = 50; повышающая передача νF = 0,65+0,11(1/U) =
= 0,65+0,11·(1/0,472) = 0,883.
С учётом всех коэффициентов напряжения изгиба в зубе колеса равны
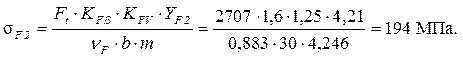
Рассчитанные напряжения изгиба меньше допускаемых (382 МПа). Условие изгибной прочности выполняется.
В случае, если напряжения окажутся больше допускаемых, можно увеличить модуль зацепления m, и/или увеличить ширину зубчатого венца b. При этом следует скорректировать геометрические параметры колёс с учётом новых параметров (m или b) и уточнить напряжения изгиба в зубе колеса.
По результатам расчёта выполняем рабочие чертежи колёс (рис. 3.25).
Дата добавления: 2020-06-09; просмотров: 597;











