Тяговый привод тепловоза ТЭП60

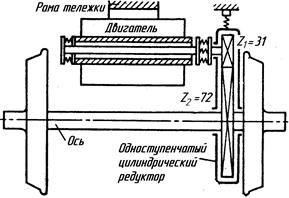
Рис. 3.5. Силовой привод ТЭП60

Рассмотрим методику расчёта цилиндрической закрытой зубчатой передачи на примере индивидуального тягового привода ведущей колёсной пары тепловоза ТЭП60 [2].

Конструкция этого привода с опорно-рамным подвешиванием тягового двигателя легко позволяет применять одноступенчатый редуктор, состоящий из прямозубой цилиндрической передачи (рис. 3.5).

Ведущая шестерня тягового редуктора, закреплённая на валу двигателя, имеет двусторонний скос по длине зуба. Зубчатый венец ведомого колеса выполнен из стали 45ХН и закреплён на кольцевом бурте поводка упругой муфты горячей посадкой с натягом 0,65…0,15 мм, а также призонными болтами из ст40. Зубья венца закалены токами СВЧ на глубину 2…5 мм.

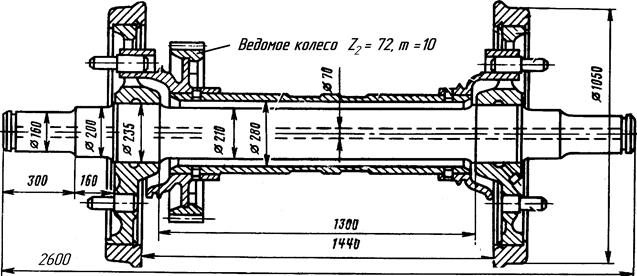
Рис. 3.6. Размеры деталей колёсной пары ТЭП60

Зубчатая передача заключена в сварной листовой кожух, куда залито 3,5 л специальной морозостойкой смазки, предназначенной для работы в условиях высоких контактных напряжений (рис. 3.6).

Пробег локомотива до капремонта не менее 1 миллиона километров.

Диаметр ведущих колёс D_к = 1050 мм. Скорость при длительном режиме V_k = 45 км/ч = 12,5 м/с (n₂ = 60V_k/πD_к = 60·12,5/3,14·1,05 =227 об/мин), максимальная V_k = 160 км/час = 44,4 м/с (n₂ = 808 об/мин).

Частота вращения вала двигателя (и шестерни) на длительном режиме
n₁ = 530 об/мин, и максимальная n₁ = 1880 об/мин.

Найдём необходимое передаточное отношение передачи: U = n₁/n₂ =
= 1880/808 = 2,32. Такое значение не соответствует нормальному ряду, следовательно, будем проектировать передачу с нестандартным передаточным отношением.

Сила тяги при длительном режиме F = 15600 кГ (153036 Н), максимальная при трогании с места F = 41600 кГ (408096 Н). Этим силам тяги соответствуют вращающий момент на оси ведущей колёсной пары при длительном режиме M₂ = F·D_к/2 = 80343900 Нмм; и при максимальном режиме трогания с места M₂ = 214250400 Нмм. Этот момент создаётся шестью одинаковыми тяговыми приводами, следовательно, вращающий момент на каждом ведомом зубчатом колесе при длительном режиме M₂ = F·D_к/(2·6) = 13390650 Нмм, на максимальном режима трогания с места M₂ = 35708400 Нмм. Все расчёты выполняются для максимальных нагрузок.

Межосевое расстояние должно находиться в конструктивных пределах от 500 до 550 мм.

Осевые силы в передаче нежелательны, поэтому колёса – прямозубые.

Шестерня и колесо расположены несимметрично относительно опор.

По этим исходным данным выполняем расчёт передачи в следующем порядке [49].

Выбираем материал для изготовления шестерни и колеса (табл. 3.1).

Если заданием не предусматривается специальных требований к габаритам и массе передачи, то можно выбирать стали со средними механическими характеристиками и относительно невысокой стоимостью.

Однако в нашем случае для тяговой передачи локомотива, требующей высокой надёжности, мы выбираем:

– для ведущей шестерни: сталь 12Х2Н3А с цементацией, НВ600, HRC56 предел контактной выносливости σ_Нlim1 = 23∙HRC = 23∙56 = 1288 МПа; коэффициент контактной безопасности S_Н1 = 1,2; предел изгибной выносливости σ_Flim1 = = 800 МПа; коэффициент изгибной безопасности S_F1 = 2,2;

– для ведомого колеса: сталь 45ХН с поверхностной закалкой НВ540, HRC55 предел контактной выносливости σ_Нlim2 = 1020 МПа; коэффициент контактной безопасности S_Н2 = 1,1; предел изгибной выносливости σ_Flim2 = 550 МПа; коэффициент изгибной безопасности S_F2 = 1,7.

Передача реверсивная, колёса стальные, следовательно, коэффициент K_FC, учитывающий реверсивность нагрузки передачи, равен 0,72 для обоих колёс.

Рассчитываем базовое число циклов контактных напряженийN_HO:

− для шестерни N_HO1 = 30 НВ^2,4 = 30 · 600^2,4 = 1,40 · 10⁸;

− для колеса N_HO2 = 30 НВ^2,4 = 30 · 540^2,4 = 1,08 · 10⁸.

Базовое число циклов изгибных напряжений N_FO1 = N_FO2 = 4·10⁶.

Фактическое число циклов напряженийN_HE:задан ресурсный пробег локомотива L ≥ 1 млн. км (10¹² мм), что при диаметре колеса 1050 мм соответствует количеству оборотов колёсной пары N = L/(πD_к) = 10¹²/(3,14·1050) = = 0,30·10⁹ оборотов. Ведомое колесо насажено на ось колёсной пары, значит, каждый его зуб нагружается один раз за оборот, т.е. наработка каждого зуба ведомого колеса N_HE2 = N_FE2 = 0,30·10⁹ циклов и каждого зуба шестерни N_HE1 = N_FE1 =N_НE2·U= 0,3·10⁹·2,32 = 0,696·10⁹ циклов. Видим, что расчётные числа циклов нагружения зубчатых колёс больше базовых.

Рассчитываем коэффициенты долговечности (см. разд. 3.2):

K_HL1 = (N_HO1/N_HE1)^1/20 = (1,4·10⁸/0,696·10⁹)^1/20 = 0,923;

K_HL2 = (N_HO2/N_HE2)^1/20 = (1,08·10⁸/0,31· 10⁹)^1/20 = 0,948;

K_FL1 = (N_FO1/N_FE1)^1/9 = (4·10⁶/0,696·10⁹)^1/9 = 0,563; примем 1;

K_FL2 = (N_FO2/N_FE2)^1/9 = (4·10⁶/0,30·10⁹)^1/9 = 0,618; примем 1.

Вычисляем допускаемые контактные напряжения:

[σ_Н]₁ = (σ_Нlim1 /S_H1)·K_HL1 = (1288/1,2)·0,923 = 990 МПа,

[σ_Н]₂ = (σ_Нlim2 /S_H2)·K_HL2 = (1020/1,1)·0,948 = 879 МПа.

Вычисляем допускаемые напряжения при изгибе:

[σ_F]₁= (σ_Flim1 /S_F1)·K_FC1·K_FL1 = (800/2,2)·0,72·1 = 261 МПа,

[σ_F]₂ = (σ_Flim2 /S_F2)·K_FC2·K_FL2 = (550/1,2)·0,72·1 = 330 МПа.

Принимаем угол наклона линии зуба β. В нашем случае передача задана, как прямозубая, т.е. β = 0.

Определяем минимальное межосевое расстояние передачи, требуемое из условия контактной прочности. В общем виде формула выглядит, как:

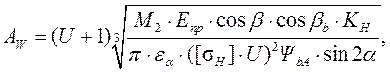
где К_Н – коэффициент нагрузки, учитывающий дополнительные вред­ные нагрузки, сопутствующие работе передачи; предварительно принимается К_Н = 1,2 для колес с твердостью поверхностей зубьев ≤ НВ350 и 1,35 для зубьев с твердостью > НВ350; E_пр – приведённый модуль упругости

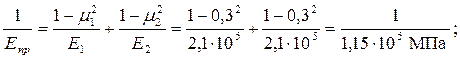
β – угол наклона зуба, β = 0, т.к. передача прямозубая; α – угол зацепления для большинства колёс принимаемый 20° (sin2α= 0,643); β_b – угол наклона линии зуба к образующей основного цилиндра β_b = arcsin ( sinβ · cosα) ==arcsin(sin0°·cos20°) = 0°; ε_α =1,05…1,1 – коэффициент перекрытия, примем ε_α =1,07; Ψ_bА – коэффициент ширины венца зубчатого колеса (табл. 3.10), для колёс нашей передачи с твёрдостью > HB350 и несимметричным расположением принимаем Ψ_bА = 0,25;

[σ_Н]− расчётное допускаемое контактное напряжение, которое равно:

− для прямозубых колёс при β = 0 [σ_Н] = [σ_Н]_min;

− для всех косозубых колёс, а также для тех прямозубых, с большой разностью твёрдостей шестерни и колеса (HB₁−HB₂) ≥ 70

[σ_Н] = 0,45([σ_Н]₁ + [σ_Н]₂).

В рассчитываемой передаче β = 0 и (HB₁−HB₂) < 70 и мы принимаем [σ_Н] =[σ_Н]_min = 879 МПа.

Таким образом, минимальное межосевое расстояние передачи, требуемое из условия контактной прочности равно:

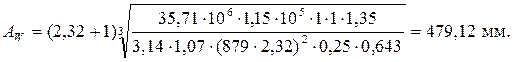
Корректируя с учётом параметрического ряда межосевых расстояний (табл. 3.12), принимаем в заданном диапазоне конструктивных ограничений (500 мм < А_W < 550 мм) большее межосевое расстояние передачи А_W = 520 мм.

Определяем числа зубьев: шестерни по условию неподрезания Z₁ >17cos³β,округляется до большего целого, примем Z₁ = 18; колеса Z₂ = Z₁·U = 18·2,32 =
= 41,76 ≈ Z₂ = 42. Уточняем передаточное отношение U_(уточн) = Z₂/Z₁ = 42/18 =
= 2,33, которое не должное отличаться от требуемого U более чем на 3%.
В нашем случае Δ = (2,33−2,32)/2,32 = 0,43%.

Определяем модуль зацепления

m = (2·A_W·cosβ)/(Z₁+Z₂) =2·520·1/(18+42) = 17,33 мм.

Однако для современных локомотивов модули тяговых передач традиционно стремятся унифицировать в пределах m = 10…11. Поэтому примем большее число зубьев Z₁ = 31, Z₂ = Z₁·U =31·2,32 = 71,92 ≈ 72. Уточнённое передаточное отношение U_(уточн) = Z₂/Z₁ =72/31 = 2,3225 отличается от заданного на
Δ = (2,3225−2,32)/2,32 = 0,001075 = 0,1075% < 3 %.

При таких числах зубьев модуль зацепления

m = (2·A_W ·cosβ)/(Z₁+Z₂) =2·520·1/(31+72) = 10,09 мм.

Из стандартного ряда (табл. 3.11) принимаем m = 10 мм. Такой модуль имеет большинство тяговых передач локомотивов.

В нашем случае рассчитывается прямозубая передача с модулем m, а для косозубых колёс здесь и далее используется нормальный модульm_n.

Уточняем межосевое расстояние передачи А_W = 0,5(Z₁ + Z₂)m/cosβ =
= 0,5(31+72)∙10/1 = 515 мм. В случае, если получается дробное число, то за уточненное значение принимаем его целую часть.

Для косозубой передачи уточняем угол наклона линии зуба

β = arccos [0,5(Z₁+Z₂)m /А_W].

Рассчитываем геометрические параметры зубчатой передачи.

Делительные диаметры: d_W1 = m · Z₁ / cosβ = 10 · 31 / 1 = 310 мм;

d_W2 = m · Z₂ / cosβ = 10 · 72 / 1 = 720 мм.

Диаметры вершин: d_a1 = d₁ + 2· m = 310 + 2 · 10 = 330 мм;

d_a2 = d₂ + 2· m = 720 + 2 · 10 = 740 мм.

Диаметры впадин: d_f1 = d₁ – 2,5 · m = 310 – 2,5 · 10 = 285 мм;

d_f2 = d₂ – 2,5 · m = 720 – 2,5 · 10 = 695 мм.

Ширина колеса Ψ_bA · А_W = 0,25 · 520 = 130 мм.

Ширина шестерни b₁ = 1,12 · b₂ = 1,12 · 130 = 145,6 мм.

Из конструктивных соображений примем b₁ = b₂ = 140 мм.

Коэффициент ширины шестерни Ψ_bd = b₂ / d_W1 = 140 / 310 = 0,45.

Определяем окружную скорость на делительном диаметре колес.

При максимальных частотах вращения двигателя n_{дв max} = 1880 об/мин:

V_max = (π ·d_W1·n_max)/60 000 = (3,14 · 310 ·1880) /60 000 = 30,4 м/с.

При длительном режиме n_{дв длит} = 530 об/мин:

V_длит = (π ·d_W1·n_длит)/60 000 = (3,14 · 310 ·530) /60 000 = 8,6 м/с.

Принимаем степень точности передачи с учетом рекомендаций для работы при длительном режиме – седьмую (табл. 3.9).

Уточняем значения коэффициентов нагрузки.

Коэффициент, учитывающий распределение нагрузки (табл. 3.2), для прямозубых колёс К_Hα = 1.

Коэффициент, учитывающий концентрацию нагрузки K_Hβ (табл. 3.3), для нашей передачи примем K_Hβ = 1,10.

Коэффициент, учитывающий динамичность приложения нагрузки K_HV (табл. 3.4), для нашей передачи примем K_HV = 1,20.

Производим проверочный расчет контактных напряжений на рабочих поверхностях зубьев. В общем случае формула записывается в виде:

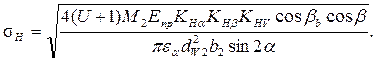
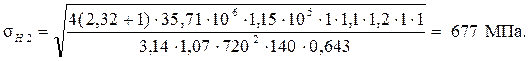
Контактные напряжения 677 МПа меньше допускаемых (879 МПа).

Находим силы, действующие в зацеплении зубчатых колес.

Окружная сила: F_t = 2 · М₂ / d_W2 = 2 · 35708400/720 = 99190 Н.

Радиальная сила: F_r = F_t tg20°/cosβ = 99190·0,364/1 = 36105 Н.

Осевая сила: F_a = F_t tg β = 99190 · 0 = 0 H (передача прямозубая).

Определяем коэффициенты прочности зубьев шестерни и колеса:

для шестерни (Z₁ = 31) Y_F1 = 3,8; для колеса (Z₂ = 72) Y_F2 = 3,61.

Определяем коэффициент наклона зуба Y_β = 1− β/140° = 1 – 0/140 = 1.

Определяем коэффициенты нагрузки для расчета зубьев на изгиб.

Коэффициент распределения нагрузки (табл. 3.5) для нашей прямозубой передачи К_Fα= 1.

Коэффициент концентрации нагрузки K_Fβ (табл. 3.6) К_Fβ= 1,04.

Коэффициент динамичности нагрузки K_FV (табл. 3.7) K_FV = 1,22.

Определяем отношения допускаемых напряжений изгиба к коэффициентам формы: [σ_F]₁ /Y_F1 =147/3,8 = 38,68 МПа; [σ_F]₂ /Y_F2 =203/3,61 = 56,23 МПа.

Производим проверочный расчет напряжений изгиба в опасном сечении зубьев шестерни, т.к. отношение [σ_F]₁/Y_F1 < [σ_F]₂/Y_F2.

σ_F1 = (Y_F1·Y_β·F_t·К_Fα·К_Fβ·К_FV)/(b₁·m).

При трогании с места: σ_F1 = (3,8·1·99190·1·1,04·1,22)/(140·10) = 341,5 МПа.

На длительном режиме: σ_F1 = (3,61·1·37149·1·1,04·1,22)/(140·10) = 127,8 МПа.

Работа локомотива в режиме трогания кратковременна, скачки вращающего момента сглаживаются специальной конструкцией привода с опорно-рамным подвешиванием и двумя упругими муфтами на входе и на выходе из редуктора. Поэтомуривода с опорно-рамным подвешиванием и двумя упругими муфтами на входе и на выходе из редуктора. опускаемыми напряжениями на изоэтому величина нагрузки на зубья может считаться постоянной, а изгибные напряжения следует сравнивать с пределом выносливости на изгиб при отнулевом цикле σ_Flim1 = 550 МПа, приведённом в таблице 3.1. Условие прочности на пусковом режиме (341,5 МПа < 550 МПа) выполняется.

Длительный режим, напротив, характерен многоцикловым нагружением зубьев, поэтому здесь изгибные напряжения следует сравнивать с допускаемыми напряжениями на изгиб, учитывающими фактические условия нагружения [σ_F]₁ = 261 МПа. Видим, что условие изгибной прочности на длительном режиме (127,8 МПа < 261 МПа) также выполняется.

Здесь имеется примерно двукратный запас по напряжениям изгиба. Для силовых передач локомотивов это обстоятельство только улучшает надёжность машины. Однако при проектировании различных механизмов, для уменьшения габаритов и веса можно уменьшить модуль при том же межосевом расстоянии, если запас прочности по изгибным напряжениям это позволяет.

При уменьшении модуля необходимо:

Подсчитать суммарное число зубьев Z_Σ = 2 · А_W · cosβ / m_n; числа зубьев колёс Z₁ = Z_Σ / ( U +1) ; Z₂ = Z₁ · U, принимая ближайшие целые.

Уточнить передаточное число U = Z₁ / Z₂ и проверить его расхождение с заданным, не более 3%.

Уточнить угол наклона зуба для косозубой передачи

β = arccos [ 0,5 (Z₁ +Z₂) m / А_W].

Пересчитать уточнённые размеры колёс:

d_W1 = m · Z₁ / cosβ; d_W2 = m · Z₂ / cosβ; d_a1 = d₁ + 2 · m;

d_a2 = d₂ + 2 · m; d_f1= d₁ – 2,5 · m; d_f2= d₂ – 2,5 · m; b₂; b₁; Ψ_bd.

Повторить расчёт контактных напряжений

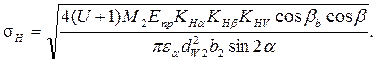
Повторно определить силы в зацеплении

F_t = 2 · М₂/d₂; F_r = F_t · tg α/cos β; F_a = F_t · tg β.

Заново определить коэффициенты формы и коэффициент наклона зуба

Y_F1; Y_F2; Y_β = 1− β/140º.

Определить коэффициенты нагрузки для нового колеса К_Fα; К_Fβ; К_FV.

Повторно рассчитать отношения [σ_F]₁/Y_F1 и [σ_F]₂/Y_F2.

Повторить проверочный расчёт напряжений изгиба в опасном сечении зубьев того колеса, где отношение [σ_F] /Y_F меньше.

Когда рассчитанные колеса принимаются к проектированию, то выполняются их рабочие чертёжи (рис. 3.7).

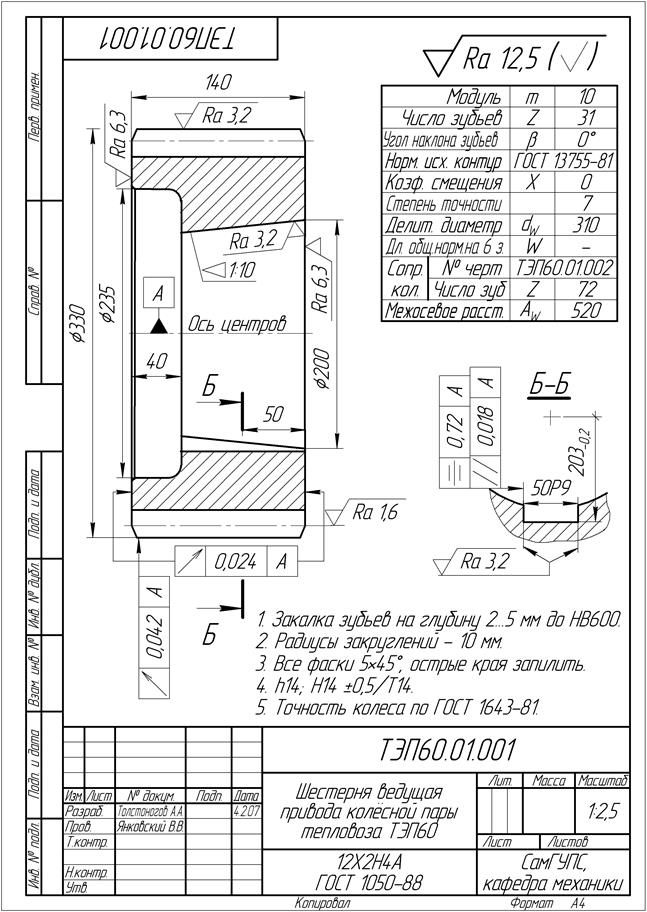
Рис. 3.7. Образец рабочего чертежа ведущей шестерни