Загальні властивості збіжних послідовностей.
Теорема 1. (Єдиність границі послідовності). Якщо послідовність має границю, то вона єдина.
Теорема 2. (Необхідна умова збіжності послідовності). Якщо послідовність збіжна, то вона обмежена.
Теорема 3. Якщо 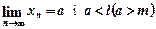 , то існує такий номер N, що при всіх
, то існує такий номер N, що при всіх 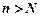 виконується нерівність
виконується нерівність 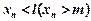 .
.
Приклад. Послідовність 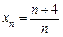 у розгорнутому вигляді така:
у розгорнутому вигляді така: 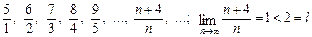 . Для номерів
. Для номерів 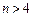 усі члени послідовності
усі члени послідовності 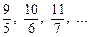 будуть менші за 2.
будуть менші за 2.
Теорема 4. Границя сталої величини дорівнює сталій, тобто 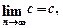
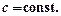
3. Теореми, які полегшують знаходження границь послідовностей.
Теорема 1. (Граничний перехід у нерівності).
Якщо для будь-якого n виконується нерівність 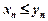 і
і 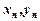 — збіжні, то
— збіжні, то 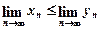 .
.
Теорема 2. (Про границю затисненої послідовності). Якщо для будь-якого n 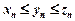 і
і 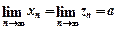 , то
, то 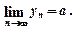
Приклад. 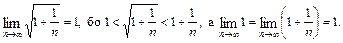
Теорема 3. (Вейєрштрасса). Про границю монотонної й обмеженої послідовності:
1) якщо монотонно зростаюча послідовність обмежена зверху, то вона збіжна;
Якщо монотонно спадна послідовність обмежена знизу, то вона збіжна.
Приклад. Довести, що 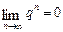 при
при 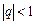 . При
. При 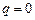 доведення очевидне. Нехай
доведення очевидне. Нехай 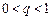 , тоді послідовність
, тоді послідовність 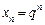 — монотонно спадна (див. рис. 3.8) і обмежена знизу
— монотонно спадна (див. рис. 3.8) і обмежена знизу 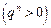 . Отже, за теоремою Вейєрштрасса послідовність
. Отже, за теоремою Вейєрштрасса послідовність 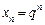 має границю, яку позначимо так:
має границю, яку позначимо так: 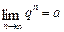 . Послідовність
. Послідовність 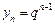 , за винятком першого члена, збігається з послідовністю
, за винятком першого члена, збігається з послідовністю 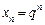 , отже,
, отже, 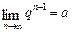 . Звідси випливає, що
. Звідси випливає, що 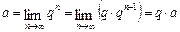 , тобто
, тобто 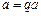 або
або 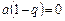 , але
, але 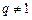 , отже,
, отже, 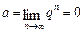 . Нехай тепер
. Нехай тепер 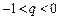 .
.
Розглянемо
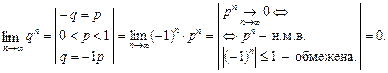
Приклад.
Тема 7. Похідна функції
План
1. Означення похідної.
2. Основні правила диференціювання.
3. Похідні від основних елементарних функцій.
4. Похідні вищих порядків.
Означення похідної
Нехай функція 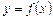 визначена на деякому проміжку (а; b). Візьмемо значення
визначена на деякому проміжку (а; b). Візьмемо значення 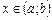 і надамо аргументу приросту
і надамо аргументу приросту 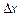 . Тоді функція набуде приросту
. Тоді функція набуде приросту 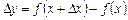 . Розглянемо відношення приросту функції
. Розглянемо відношення приросту функції 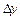 до приросту аргументу
до приросту аргументу 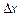 і перейдемо до границі при
і перейдемо до границі при 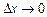 :
:
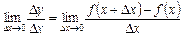 . (7.1)
. (7.1)
Якщо границя (4.1) існує і скінченна, вона називається похідною функції 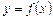 за змінною х і позначається
за змінною х і позначається
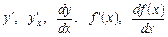 .
.
Означення. Похідною функції 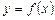 за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
Операція знаходження похідної називається диференціюванням цієї функції.
Користуючись означенням похідної, знайти похідні функцій.
Приклад. Функція у = х2. Знайти похідну в точках х = 3 і х = – 4.
l Надамо аргументу х приросту 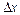 , тоді функція набуде приросту
, тоді функція набуде приросту 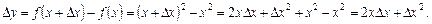
Складемо відношення приросту функції до приросту аргументу 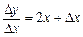 , відшукаємо границю
, відшукаємо границю 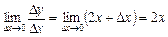 . Таким чином,
. Таким чином, 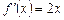 .
.
Похідна в точці х = 3 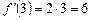 , а похідна при х = – 4 буде
, а похідна при х = – 4 буде 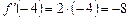 .
.
Приклад. 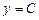 , де
, де 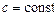 .
.
l Надавши аргументу 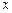 приросту
приросту 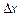 , дістанемо приріст функції
, дістанемо приріст функції 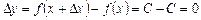 . Тепер знайдемо границю відношення
. Тепер знайдемо границю відношення 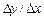 при
при 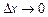 :
:
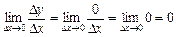 , тобто
, тобто 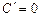
Приклад. 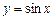 .
.
l Користуючись відомою з тригонометрії формулою
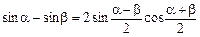 ,
,
знайдемо приріст функції у точці 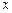 і обчислимо границю:
і обчислимо границю:
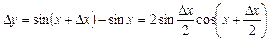 ,
,
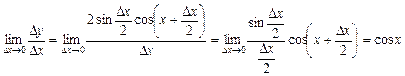 ;
;
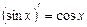 .
.
Аналогічно можна дістати: 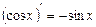 .
.
Приклад. 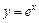 .
.
l Для цієї функції маємо
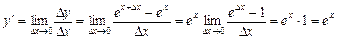 ,
,
тобто 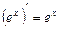 .
.
Дата добавления: 2016-05-26; просмотров: 5069;











