Поняття числової послідовності та її границі
Означення. Числова функція 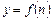 , область визначення якої є множина натурального ряду чисел, називається числовою послідовністю, або просто послідовністю, і позначається
, область визначення якої є множина натурального ряду чисел, називається числовою послідовністю, або просто послідовністю, і позначається 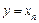 , надалі писатимемо
, надалі писатимемо 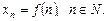
Значення 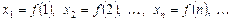 називаються членами послідовності. Послідовність вважається заданою, якщо задано n-й член послідовності.
називаються членами послідовності. Послідовність вважається заданою, якщо задано n-й член послідовності.
Приклад. Записати три перші члени послідовності 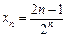 . Маємо
. Маємо 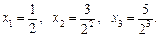
Приклад. За заданими трьома першими членами послідовності 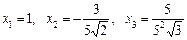 знайти формулу n-го члена.
знайти формулу n-го члена.
Задача розв’язується методом добору з наступною перевіркою 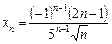 .
.
Означення. Число а називається границею послідовності 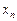 , якщо для будь-якого
, якщо для будь-якого 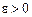 , яке б мале воно не було, існує номер N такий, що для всіх номерів
, яке б мале воно не було, існує номер N такий, що для всіх номерів 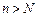 виконується нерівність
виконується нерівність 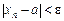 .
.
Позначення 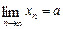 або
або 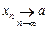 .
.
Для стислого запису означення границі використаємо квантори: " — для будь-якого, будь-який; $ — існує, знайдеться;
: = дорівнює за означенням, означає. Тоді означення границі послідовності за допомогою цих символів запишеться так:
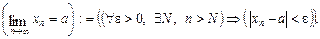
Розглянемо геометричну інтерпретацію границі послідовності. На числовій осі побудуємо e-окіл числа а, тобто інтервал (а – e; а + e), і покажемо, як розміщуватимуться точки, які відповідають членам послідовності 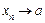 , при
, при 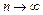 (рис. 3.12).
(рис. 3.12).
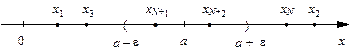
| Рис. 6.1 |
Означення. Число а називається границею послідовності xn, якщо для будь-якого e-околу точки а існує номер N такий, що, починаючи з номерів 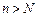 , усі члени послідовності перебувають в e-околі точки а (див. рис. 6.1).
, усі члени послідовності перебувають в e-околі точки а (див. рис. 6.1).
Означення. Послідовність називається збіжною, якщо вона має границю (скінченну). Послідовність, яка не має границі, називається розбіжною.
Приклад. Довести за означенням, що 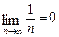 .
.
Зауважимо, що n-й член послідовності 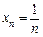 ; сама послідовність така:
; сама послідовність така: 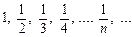 . Для доведення потрібно за заданим
. Для доведення потрібно за заданим 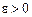 знайти номер послідовності N,такий, що при всіх номерах
знайти номер послідовності N,такий, що при всіх номерах 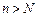 виконуватиметься нерівність
виконуватиметься нерівність 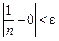 . Розв’яжемо останню нерівність відносно n:
. Розв’яжемо останню нерівність відносно n:
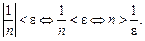
Виберемо* 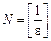 . Тоді при
. Тоді при 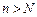 нерівність
нерівність 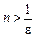 виконується, а отже, виконується і нерівність
виконується, а отже, виконується і нерівність 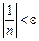 , чим доведено, що
, чим доведено, що 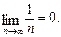 Отже, для доведення за означенням певної границі послідовності досить побудувати функціональну залежність N від числа e, тобто знайти функцію N(e). У розглянутому прикладі функція
Отже, для доведення за означенням певної границі послідовності досить побудувати функціональну залежність N від числа e, тобто знайти функцію N(e). У розглянутому прикладі функція 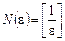 , і за заданим будь-яким
, і за заданим будь-яким 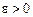 завжди можна знайти відповідний номер N; наприклад при
завжди можна знайти відповідний номер N; наприклад при 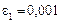 ,
, 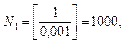 при
при 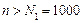 нерівність
нерівність 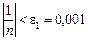 виконується.
виконується.
Дата добавления: 2016-05-26; просмотров: 2351;











