Основні правила диференціювання
Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то 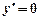 .
.
Теорема 2. Похідна алгебраїчної суми скінченної кількості диференційовних функцій дорівнює алгебраїчній сумі похідних цих функцій: 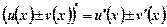 .
.
Теорема 3. Похідна добутку двох диференційовних функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:
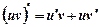 .
.
Теорема 4. Сталий множник можна виносити за знак похідної:
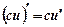 , де
, де 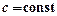 .
.
Теорема 5. Якщо чисельник і знаменник дробу диференційовні функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різницею добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадратом знаменника початкового дробу 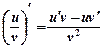 .
.
Зауваження. Похідну від функції 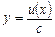 , де
, де 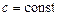 , зручно обчислювати як похідну від добутку сталої величини
, зручно обчислювати як похідну від добутку сталої величини 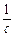 на функцію u (x):
на функцію u (x):
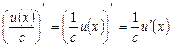 .
.
Приклад. Обчислити похідну для функції у = tg x.
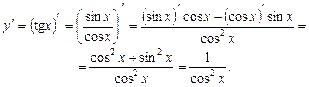
Таким чином, 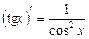 .
.
Похідна складної функції.Нехай у = f (u), де 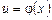 , тобто
, тобто 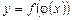 . Функція f (u) називається зовнішньою, а функція
. Функція f (u) називається зовнішньою, а функція 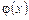 — внутрішньою, або проміжним аргументом.
— внутрішньою, або проміжним аргументом.
Теорема 6. Якщо у = f (u) та 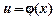 — диференційовні функції від своїх аргументів, то похідна складної функції існує і дорівнює
— диференційовні функції від своїх аргументів, то похідна складної функції існує і дорівнює 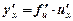 .
.
Таким чином, похідна складної функції дорівнює добутку похідної зовнішньої функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною.
Похідна неявної функції.Нехай рівняння F (x; y) = 0 визначає у як неявну функцію від х. Надалі будем вважати, що ця функція — диференційовна.
Продиференціювавши за х обидві частини рівняння F (x; y) = 0, дістанемо рівняння першого степеня відносно 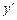 . З цього рівняння легко знайти
. З цього рівняння легко знайти 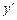 , тобто похідну неявної функції.
, тобто похідну неявної функції.
Приклад. Знайти 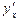 з рівняння
з рівняння 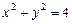 .
.
l Оскільки у є функцією від х, то у2 розглядатимемо як складну функцію від х, тобто 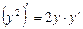 .
.
Продиференціювавши по х обидві частини заданого рівняння, дістанемо 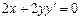 . Звідси
. Звідси 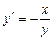 .
.
Похідна оберненої функції.Нехай задані дві взаємно обернені диференційовні функції
у = f (х) та 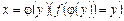 .
.
Теорема 7. Похідна 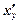 оберненої функції
оберненої функції 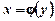 по змінній у дорівнює оберненій величині похідної
по змінній у дорівнює оберненій величині похідної 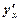 від прямої функції
від прямої функції 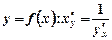 .
.
Приклад. Обчислити похідну для функції 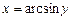 .
.
l Задана функція обернена до функції 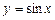 . Згідно з теоремою 7 можна записати
. Згідно з теоремою 7 можна записати
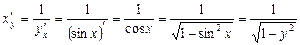 .
.
Звідси 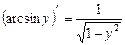 .
.
Якщо в останньому виразі замість у записати х, то дістанемо
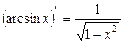 .
.
Дата добавления: 2016-05-26; просмотров: 2295;











