Похідні від основних елементарних функцій
За аналогією з попередніми прикладами можна дістати похідні від основних елементарних функцій:
1. 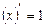 ; 2.
; 2. 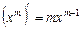 ;
;
3. 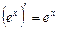 ; 4.
; 4. 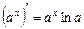 ;
;
5. 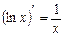 ; 6.
; 6. 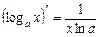 ;
;
7. 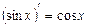 ; 8.
; 8. 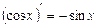 ;
;
9. 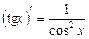 ; 10.
; 10. 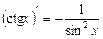 ;
;
11. 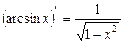 ; 12.
; 12. 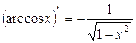 ;
;
13. 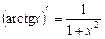 ; 14.
; 14. 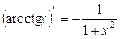 .
.
Продиференціювати подані далі функції.
Приклад. 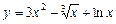 .
.
l Дана функція є алгебраїчною сумою функцій, тому використовуємо теорему 2:
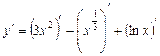 .
.
У здобутому виразі перший доданок алгебраїчної суми є добуток сталої величини на степеневу функцію Þ — застосуємо до нього теорему 4 і формулу (2) таблиці похідних; другий — ірраціональна функція з показником 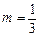 — застосуємо формулу (2) таблиці похідних; третій — логарифмічна функція з основою е Þ — використаємо формулу (5):
— застосуємо формулу (2) таблиці похідних; третій — логарифмічна функція з основою е Þ — використаємо формулу (5):
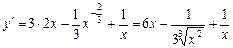 .
.
Приклад. 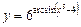 .
.
l Задана функція складна: зовнішня — показникова функція з основою 6, внутрішня для неї — обернена тригонометрична. Обернена тригонометрична, у свою чергу, є складною, для якої внутрішня функція — алгебраїчна сума 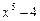 . Для суми аргументом (скінченним) є х.
. Для суми аргументом (скінченним) є х.
Таким чином, задана функція є суперпозицією трьох функцій.
При диференціюванні послідовно застосовуємо два рази теорему 6:
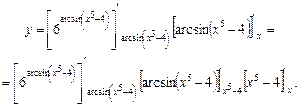
У цьому виразі знизу біля кожної квадратної дужки вказано аргумент, за яким слід диференціювати функцію, взяту в дужки.
Тепер послідовно скористаємося формулами (4), (11), (2) таблиці похідних та теоремами 1, 2. Дістанемо:
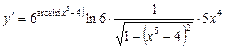 .
.
Взагалі використані правила та формули не фіксують, а записують кінцевий результат їх застосування.
Приклад. 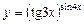 .
.
l Задана функція є степенево-показниковим виразом виду
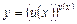 , де
, де 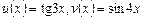 . (7.5)
. (7.5)
Прологарифмуємо функцію (4.5) за основою е:
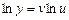 . (7.6)
. (7.6)
Оскільки 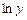 і
і 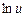 — складні функції, після диференціювання обох частин рівності (4.6) дістанемо:
— складні функції, після диференціювання обох частин рівності (4.6) дістанемо:
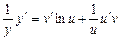 .
.
Звідси 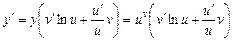 .
.
Таким чином, дістали формулу для знаходження похідної від степенево-показникової функції виду (4.5).
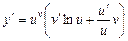 . (7.7)
. (7.7)
У даному випадку формула (4.7) виглядає як
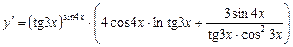 .
.
Похідні вищих порядків
Похідна 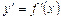 від функції
від функції 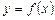 називається похідною першого порядку і являє собою деяку нову функцію. Можливі випадки, коли ця функція сама має похідну. Тоді похідна від похідної першого порядку
називається похідною першого порядку і являє собою деяку нову функцію. Можливі випадки, коли ця функція сама має похідну. Тоді похідна від похідної першого порядку 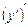 називається похідною другого порядку від функції
називається похідною другого порядку від функції 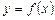 і позначається
і позначається 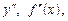
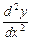 .
.
Похідна від похідної другого порядку 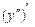 називається похідною третього порядку і означається
називається похідною третього порядку і означається 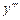 ,
, 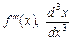 .
.
Похідна від похідної (n – 1)-го порядку 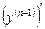 називається похідною n-го порядку і позначається
називається похідною n-го порядку і позначається 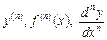 .
.
Таким чином, 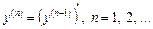
Приклад. Знайти похідну третього порядку для функції 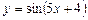 .
.
l 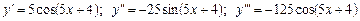 .
.
Дата добавления: 2016-05-26; просмотров: 2323;











