Несобственные интегралы
Понятие определенного интеграла вводилось и изучалось, во-первых, в предположении, что интегрируемая функция должна быть ограниченной на отрезке интегрирования, во-вторых, сам отрезок должен быть конечным. Если хотя бы одно из этих необходимых требований не выполнено, то определенный интеграл не существует.
Оказывается, существуют классы функций, для которых, хотя и нарушены указанные требования, можно говорить о существовании определенного интеграла. Естественно, при этом определенный интеграл понимается не в обычном смысле, а рассматривается некоторое его обобщение. Укажем два основных класса таких функций.
1. Несобственные интегралы первого рода.
Пусть функция f(x) определена и непрерывна на промежутке [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Если существует конечный предел 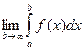 , то этот предел называется несобственным интегралом1-го рода от функции f(x) на промежутке [a, ¥).
, то этот предел называется несобственным интегралом1-го рода от функции f(x) на промежутке [a, ¥).
Обозначается: 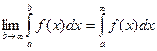
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
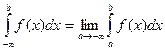
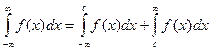
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример. 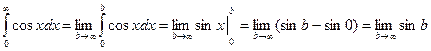 - не существует, следовательно, несобственный интеграл расходится.
- не существует, следовательно, несобственный интеграл расходится.
Пример. 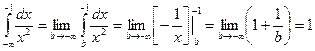 - интеграл сходится
- интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие 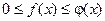 и интеграл
и интеграл 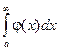 сходится, то
сходится, то 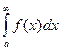 тоже сходится и
тоже сходится и 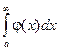 ³
³ 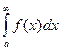 .
.
Теорема: Если для всех х (x ³ a) выполняется условие 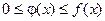 и интеграл
и интеграл 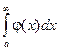 расходится, то
расходится, то 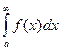 тоже расходится.
тоже расходится.
Теорема: Если 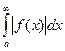 сходится, то сходится и интеграл
сходится, то сходится и интеграл 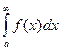 .
.
В этом случае интеграл 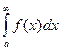 называется абсолютно сходящимся.
называется абсолютно сходящимся.
Пример. Рассмотрим несобственный интеграл 1-го рода функции 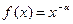 на промежутке
на промежутке 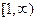 . При
. При 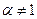 имеем:
имеем:
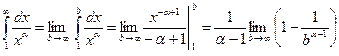 .
.
Отсюда следует, что при 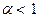 несобственный интеграл расходится, а при
несобственный интеграл расходится, а при 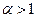 он сходится, причем
он сходится, причем 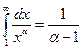 ,
, 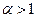 .
.
Легко убедиться, что рассматриваемый несобственный интеграл расходится и при 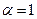 .
.
2. Несобственные интегралы второго рода.
Пусть 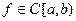 , где
, где 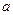 и
и 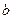 – некоторые числа, причем
– некоторые числа, причем 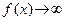 при
при 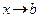 (функция неограничена). Тогда
(функция неограничена). Тогда 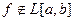 .
.
Возьмем 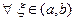 . Тогда
. Тогда 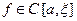 и, следовательно,
и, следовательно, 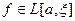 .
.
Несобственным интегралом 2-го рода функции 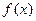 на промежутке
на промежутке 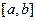 называют предел
называют предел 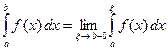 .
.
Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Так же, как и выше, определяют интеграл от функции, неограниченной в окрестности точки 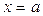 .
.
Пример. Исследовать на сходимость несобственный интеграл 2-го рода функции 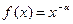 ,
, 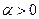 , на промежутке
, на промежутке 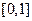 . При
. При 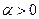 ,
, 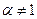 имеем:
имеем:
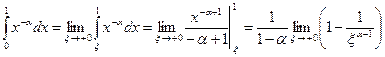 .
.
Из полученных соотношений следует, что если 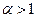 , то несобственный интеграл расходится; если же
, то несобственный интеграл расходится; если же 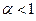 , то сходится, причем
, то сходится, причем 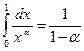 ,
, 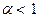 .
.
Рассматриваемый несобственный интеграл расходится и при 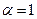 .
.
Наконец, если 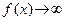 при
при 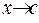 , где
, где 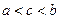 , то полагают
, то полагают
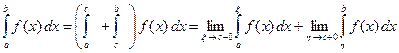 .
.
Дата добавления: 2020-06-09; просмотров: 727;











