Свойства определенного интеграла
1) При перестановке пределов изменяется знак интеграла:
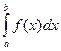 = -
= - 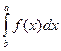
2) Интеграл с одинаковыми пределами равен нулю:
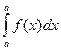 = 0
= 0
3) Отрезок интегрирования можно разбить на части:
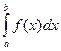 =
= 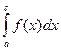 +
+ 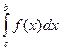
4) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов
5) Постоянный множитель можно вынести за знак определенного интеграла.
Пример. Вычислить определенный интеграл 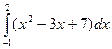
Применяя формулу Ньютона-Лейбница и свойства определенного интеграла, получим:
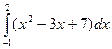 =
= 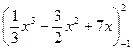 =
= 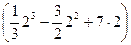 -
- 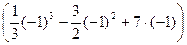 = 19,5
= 19,5
Замена переменной в определенном интеграле
Пусть задан интеграл 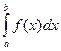 , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t). Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то
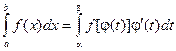
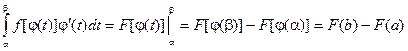
Интегрирование по частям в определенном интеграле
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
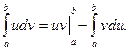
Дата добавления: 2020-06-09; просмотров: 640;











