Криволинейные и поверхностные интегралы от векторных функций
Пусть в каждой точке пространства, и в частности, на кривой (или на поверхности), задана векторная функция 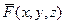 , которая состоит из 3 координатных скалярных функций и имеет вид:
, которая состоит из 3 координатных скалярных функций и имеет вид:
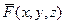 =
= 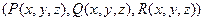 .
.
Пусть параметрически задана некоторая кривая. В каждой её точке существует вектор, расположенный на касательной, обозначаемый 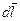 и равный
и равный 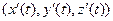 . (это хорошо известный из физики вектор скорости
. (это хорошо известный из физики вектор скорости 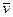 ). Если скалярно умножить
). Если скалярно умножить 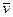 на
на 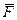 , получим числовую величину в каждой точке кривой.
, получим числовую величину в каждой точке кривой.
Определение. Пусть дана некоторая кривая в пространстве 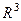 . Во всех точках пространства (и в частности, на кривой) задана ограниченная и непрерывная векторная функция
. Во всех точках пространства (и в частности, на кривой) задана ограниченная и непрерывная векторная функция 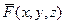 . Введём разбиение кривой на n частей, возьмём на каждой из этих частей по одной точке
. Введём разбиение кривой на n частей, возьмём на каждой из этих частей по одной точке 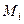 . Рассмотрим интегральную сумму:
. Рассмотрим интегральную сумму: 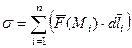 . Предел таких сумм при
. Предел таких сумм при 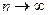 называется криволинейным интегралом 2-го рода (от векторной функции).
называется криволинейным интегралом 2-го рода (от векторной функции).
Обозначается 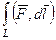
Физический смысл: работа силы по перемещению точки по кривой.
Формулы вычисления:
Краткая формула для запоминания: 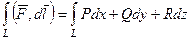 .
.
Здесь видно скалярное произведение двух векторов, у каждого из которых по 3 координаты: 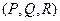 и
и 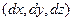 , который также можно записать в виде
, который также можно записать в виде 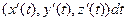 .
.
Более подробно для вычислений на практике:
1) Для параметрически заданной кривой в трёхмерном пространстве правая часть формулы пример такой длинный вид: 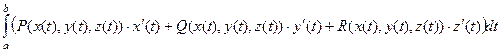 На самом деле, ничего особо сложного в вычислениях нет, надо просто в функциях
На самом деле, ничего особо сложного в вычислениях нет, надо просто в функциях 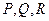 все переменные
все переменные 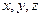 выразить через
выразить через 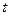 по тем формулам, которые задают параметрически кривую в пространстве. После этого всё сводится к определённому интегралу от одной переменной
по тем формулам, которые задают параметрически кривую в пространстве. После этого всё сводится к определённому интегралу от одной переменной 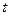 .
.
2) Для параметрически заданной кривой в плоскости: 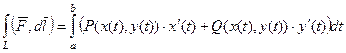 .
.
Пример.Точка движется по полуокружности радиуса 1 в верхней полуплоскости, и на неё действует сила 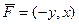 . Найти работу силы.
. Найти работу силы.
Решение.Так как все точки расположены на окружности, то задаём параметрически: 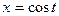 ,
, 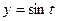 ,
, 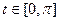 .
.
При этом 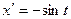 ,
, 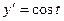 .
.
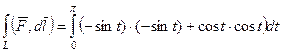 =
= 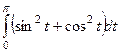 =
= 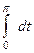 =
= 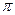 .
.
Дата добавления: 2020-03-17; просмотров: 932;











