Тема 4.6. Дифференциальные уравнения

В приложениях математики к различным отраслям науки и техники дифференциальные уравнения занимают важное место. В отличие от алгебраических уравнений в дифференциальных уравнениях по некоторым заданным функциям требуется определить функцию, которая задается своими производными. Таким образом, дифференциальными уравнениями описываются более сложные процессы, происходящие в природе и технике.

Дифференциальным уравнением называется уравнение, содержащее независимую переменную х, искомую функцию у и ее производные у′, у′′,…

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Символически дифференциальное уравнение первого порядка записывается следующим образом:

F(x, y, y′) = 0 или у′ = f(x, y)

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Пример 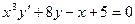- обыкновенное дифференциальное уравнение 1–го порядка.

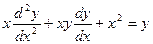- обыкновенное дифференциальное уравнение 2 – го порядка.

Решением дифференциального уравнения называется всякая функция у = φ(х), которая обращает данное уравнение в тождество.

Общим решением дифференциального уравнения называется функция у = φ(х,С), зависящая от постоянной С и удовлетворяющая данному уравнению при любом фиксированном значении этой постоянной.