Интегрирование элементарных дробей
Элементарныминазываются дроби следующих четырех типов:
I. 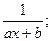 II.
II. 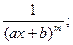 III.
III. 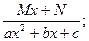 IV.
IV. 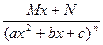
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 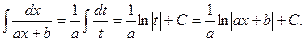
II. 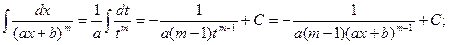
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби III вида может быть представлен в виде:
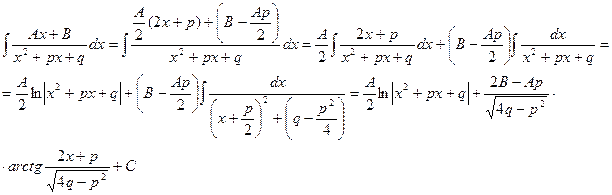
Пример. 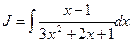
Т.к. 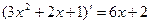 ,
, 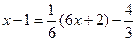 , то
, то 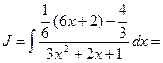
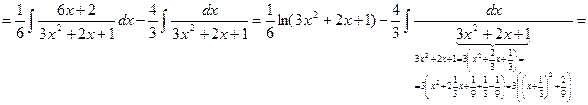
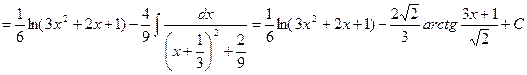
Пример. 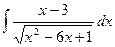
Т.к. 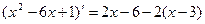 , то
, то 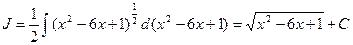
Пример. 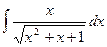
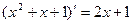 ,
, 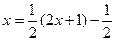
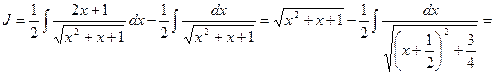
= 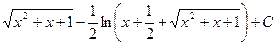
Пример. 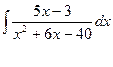
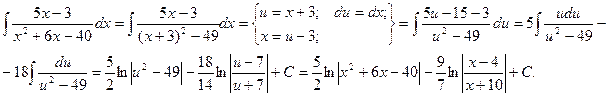
Пример. 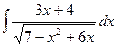
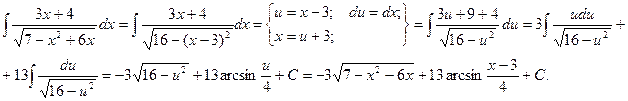
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида 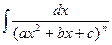 можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 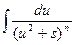 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
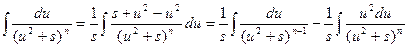 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 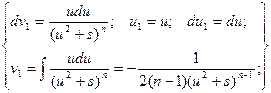
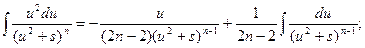
Для исходного интеграла получаем:
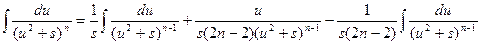
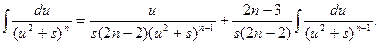
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 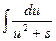 .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
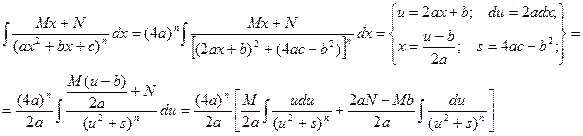
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному 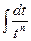 , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример:
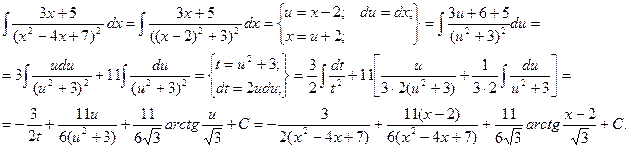
Дата добавления: 2020-06-09; просмотров: 632;











