Свойства непрерывных функций

Свойство 1. Если функция f(x, y) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется, по крайней мере, одна точка N(x₀, y₀), такая, что для остальных точек верно неравенство

f(x₀, y₀) ³ f(x, y),

а также точка N₁(x₀₁, y₀₁), такая, что для всех остальных точек верно неравенство

f(x₀₁, y₀₁) £ f(x, y),

тогда f(x₀, y₀) = M – наибольшее значение функции, а f(x₀₁, y₀₁) = m – наименьшее значение функции f(x, y) в области D.

Непрерывная функция в замкнутой и ограниченной области D достигает, по крайней мере, один раз наибольшего значения и один раз наименьшего.

Свойство 2. Если функция f(x, y) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка N₀(x₀, y₀) такая, что f(x₀, y₀) = m.

Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция, по крайней мере, один раз обращается в ноль.

Свойство 3. Функция f(x, y), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство .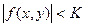

Свойство 4. Если функция f(x, y) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х₁, y₁) и (х₂, у₂) области, находящихся на расстоянии, меньшем D, выполнено неравенство

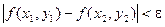
Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке.