Интегрирование по частям
Этот способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u,
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 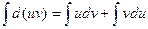 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла: 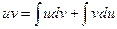 или
или
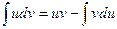 .
.
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Этот метод применяется, когда подынтегральная функция имеет вид: 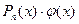 , где
, где 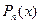 - это многочлен степени п, а
- это многочлен степени п, а 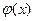 является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией.
является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией.
1. Если - показательная или тригонометрическая функция (т.е. имеем интегралы вида 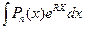 ,
, 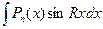 ,
, 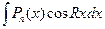 ), то для того чтобы найти эти интегралы, нужно сделать замену
), то для того чтобы найти эти интегралы, нужно сделать замену 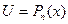
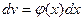 и применить формулу интегрирования по частям n раз.
и применить формулу интегрирования по частям n раз.
2. Если 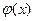 - логарифмическая или обратная тригонометрическая функция (т.е. имеем интегралы вида
- логарифмическая или обратная тригонометрическая функция (т.е. имеем интегралы вида 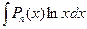 ,
, 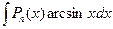 ,
, 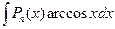 ,
, 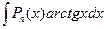 ,
, 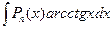 ) то для того, чтобы найти эти интегралы нужно сделать замену:
) то для того, чтобы найти эти интегралы нужно сделать замену: 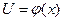 ,
, 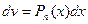 .
.
3. Интегралы вида 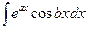 ,
, 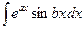 (a, b — числа) вычисляются двукратным интегрированием по частям.
(a, b — числа) вычисляются двукратным интегрированием по частям.
Пример. Вычислить 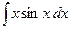 .
.
Данный интеграл относится к 1 типу.
Положим 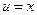 ,
, 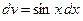 ; тогда
; тогда 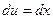 ,
, 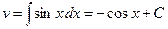 . Найдем
. Найдем 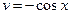 . Подставим в формулу интегрирования по частям:
. Подставим в формулу интегрирования по частям:
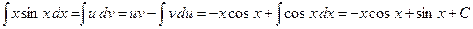 .
.
Пример. Вычислить 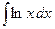 .
.
Данный интеграл относится ко 2 типу
Положим 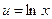 ,
, 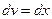 ; тогда
; тогда 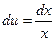 ,
, 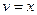 .
.
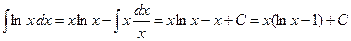 .
.
Пример. Вычислить 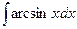
Данный интеграл относится ко 2 типу.
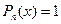 ,
, 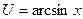 ,
, 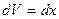
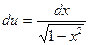 ,
, 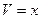
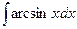 =
= 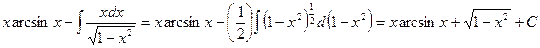
Пример. Вычислить 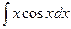
Интеграл 1 типа. Имеем 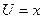 ,
, 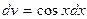
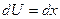 ,
, 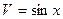
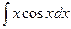 =
= 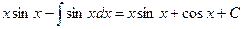
Пример. Вычислить 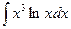
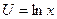 ,
, 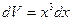 ,
, 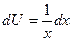 ,
, 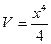
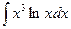 =
= 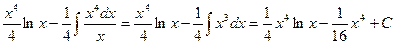
Пример. Вычислить 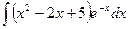
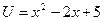 ,
, 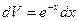 ,
, 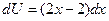 ,
, 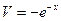
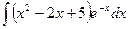 = =
= = 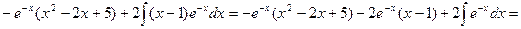
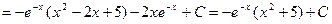 .
.
Пример. Вычислить 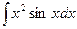
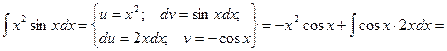
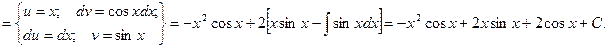
Пример. Вычислить 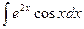
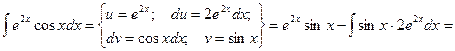
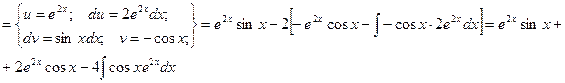
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
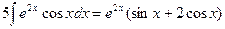
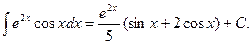
Дата добавления: 2020-06-09; просмотров: 680;











