Базис И, ИЛИ, НЕ. Свойства элементарных функций алгебры логики

Основные понятия алгебры логики

Понятие цифрового автомата было введено как модель для описания функционирования устройств, предназначенных для переработки цифровой или дискретной информации.

Для формального описания цифровых автоматов применяется аппарат алгебры логики, созданной английским математиком Дж. Булем (1815-1864). Поэтому алгебру логики называют алгеброй Буля или булевой алгеброй.

В алгебре логики применительно к описанию цифровых автоматов, работающих в двоичном представлении кодов (или цифровой информации) основными понятиями являются логическая (булева) переменная и логическая функция (функция алгебры логики - ФАЛ).

Логическая (булева) переменная - такая величина x, которая может принимать только два значения : x = {0,1}.

Логическая функция (функция алгебры логики - ФАЛ) - функция многих аргументов f(x_n-1, x_n-2,, ..., x₀), принимающая значения равные нулю или единице на наборах логических переменных x_n-1, x_n-2,, ..., x₀.

В дальнейшем в формальных описаниях наборов переменных и логических функций сами наборы переменных интерпретируются как двоичные коды (числа). В двоичных кодах расположение логических переменных упорядочено в порядке уменьшения индекса слева направо и каждая логическая переменная имеет вес в зависимости от позиции в коде, увеличивающийся справа налево. Вес каждой i - той логической переменной, являющейся значением разряда двоичного числа равен 2ⁱ (i = 0, ... , n-1).

Для n - разрядного кода общее количество уникальных наборов переменных

N = 2ⁿ; (1)

Максимальное числовое значение двоичного кода равно

A_макс = 2ⁿ-1; (2)

Значения всех логических функций от одной переменной представлены в таблице 1.Таблица 1

Функция f₀(x) называется константой нуля, а функция f₃(x) - константой единицы. Функция f₁(x), повторяющаязначения логической переменной, -тождественная функция (f₁(x) º x), а функция f₂(x), принимающая значения, обратные значениям переменной x, - логическое отрицание или инверсия (НЕ) (f₂(x) = ).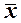

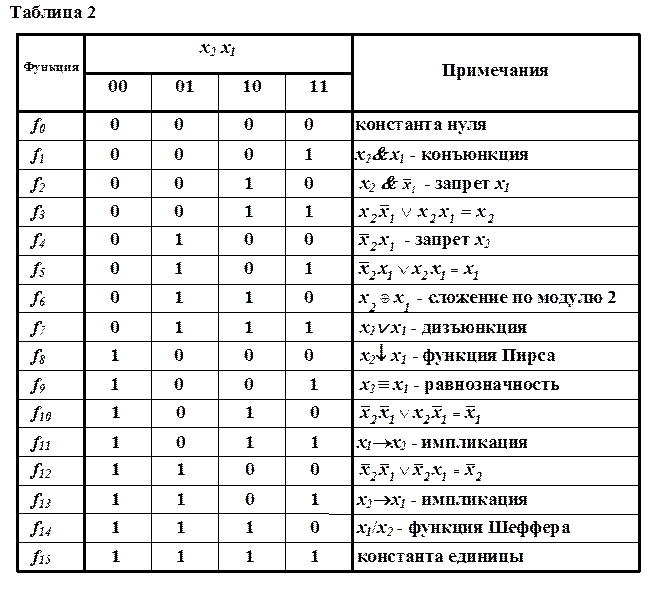
Значения всех логических функций от двух переменных представлены в таблице 2. Для функции двух переменных, согласно ф.(1), существует четыре уникальных набора переменных. Функции отличаются друг от друга набором значений 0 и 1 в четырех разрядах кода значений функции. Общее количество функций на n - местном или n - разрядном наборе переменных равно

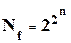; (3)

В таблице 2 приведены примеры аналитической записи некоторых булевых функций с использованием других булевых функций, то есть существует такой набор булевых функций, из которого можно сконструировать любую булеву функцию, равносильную заданной.

Две функции равносильны друг другу, если они принимают на всех возможных наборах переменных одни и те же значения.

Аналитически это свойство описывается следующей формулой:

f₁ (x_n-1, x_n-2,, ..., x₀) = f₂ (x_n-1, x_n-2,, ..., x₀); (4)

Обе функции в ф.(4) могут иметь разные формы аналитической записи, но практически наиболее выгодной будет самая простая форма записи.

Система булевых функций W называется функционально полной, если для любой булевой функции n - переменных f(x_n-1, x_n-2,, ..., x₀) может быть построена равносильная ей функция комбинированием булевых переменных x_n-1, x_n-2,, ..., x₀ и функций системы W, взятых в любом конечном количестве экземпляров каждая. Такая система булевых функций (W) называется базисом.

Таким образом, базис - полная система функций алгебры логики (ФАЛ), с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций W.

Базисом является система функций И ( конъюнкция), ИЛИ ( дизъюнкция), НЕ ( инверсия), свойства которых были впервые изучены Дж. Булем.

Базисами являются системы:

- И,НЕ;

- ИЛИ,НЕ;

- функция Шеффера И-НЕ;

- функция Пирса ИЛИ-НЕ.

Базис является минимальным, если удаление из него хотя бы одной функции превращает систему ФАЛ в неполную. Базис И, ИЛИ, НЕ - избыточный.

Базис И, ИЛИ, НЕ. Свойства элементарных функций алгебры логики

Пусть x - некоторая логическая переменная. Тогда:

1. 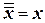, что означает возможность исключения из логического выражения всех членов, имеющих двойное отрицание, заменив их исходной величиной;

2. 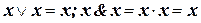- правила подобных преобразований, которые позволяют сокращать длину логических выражений;

3. xÚ0=x;

4. xÚ1=1;

5. x ^. 0=0;

6. x ^.1=x;

7. ;

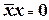8. .

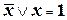Дизъюнкция и конъюнкция обладают рядом свойств, аналогичных свойствам обычных арифметических операций сложения и умножения:

1). свойство ассоциативности (сочетательный закон):

x₁Ú(x₂Úx₃)=(x₁Úx₂)Úx₃, x₁(x₂ x₃)=(x₁ x₂) x₃;

2). свойство коммутативности (переместительный закон):

x₁Úx₂=x₂Úx₁, x₁x₂=x₂ x₁;

3). свойство дистрибутивности (распределительный закон):

для конъюнкции относительно дизъюнкции

x₁&(x₂Úx₃)=(x₁&x₂)Ú(x₁&x₃);

для дизъюнкции относительно конъюнкции

x₁Úx₂&x₃=(x₁Úx₂)&(x₁Úx₃).

Свойство дистрибутивности фактически определяет правила раскрытия скобок или взятия в скобки логических выражений.

Справедливость указанных свойств легко доказывается с помощью вышеизложенных аксиом.

Докажем, например, что

x₁Úx₂&x₃=(x₁Úx₂)&(x₁Úx₃).

В самом деле, (x₁Úx₂)(x₁Úx₃) = x₁x₁Ú x₁x₃Ú x₁x₂Ú x₂x₃ = x₁Ú x₁x₂Ú x₁x₃Ú Úx₂x₃ = x₁(1Ú x₂Ú x₃) Ú x₂x₃.

Аналогично можно доказать и другие законы.

Таким же образом доказывается правильность соотношений, известных как законы де Моргана:

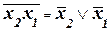, (5)

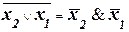. (6)

Из законов де Моргана следует, что:

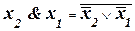. (7)

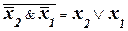, (8)

помощью которых появляется возможность выражать конъюнкцию через дизъюнкцию и отрицание или дизъюнкцию через конъюнкцию и отрицание.

Законы де Моргана и следствия из них справедливы для любого количества переменных:

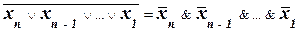, (9)

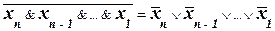. (10)

Для логических функций устанавливаются соотношения, известные как законы поглощения:

x₁Ú x₁x₂ = x₁, (11)

x₁&(x₁Úx₂) = x₁. (12)

Очень важными в теории ФАЛ являются действия полного склеивания и неполного склеивания. Примеры выполнения этих действий с двумя конституентами 1 приведены ниже:

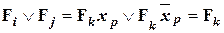- полное склеивание; (13)

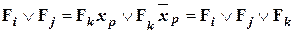- неполное склеивание. (14)

Более важным для практики является неполное склеивание, так как для сложных ФАЛ исходные конституенты 1 F_i и F_j после получения результата склеивания друг с другом F_k сохраняются для сопоставления с другими минтермами в записи заданной ФАЛ и нового склеивания по одной из переменных, входящих в сопоставимые минтермы с отрицанием и без отрицания (отличающихся по одной переменной).

Рассмотренные основные соотношения позволяют описать равносильные булевы функции различными способами, вследствие чего открываются возможности выбора самых простых форм описания ФАЛ. Самые простые по форме ФАЛ реализуются на элементной базе по принципиальным схемам, имеющим самую низкую стоимость.