Понятие неопределенного интеграла
Для дифференцирования существует обратное действие – интегрирование: отыскание функции по известной производной.
Функция F(x) называется первообразной от функции f(x) на отрезке [a;b], если во всех точках этого отрезка выполняется равенство: F′(x) = f(x).
Если функция F(x) является первообразной для функции f(x), то выражение F(x) + C называется неопределенным интегралом от функции f(x) и обозначается символом:
∫ f(x)dx.
При этом функцию f(x) называют подынтегральной функцией.
Нахождение всех первообразных для данной функции называется ее интегрированием. Если F(x) - какая-нибудь первообразная для функции f(x), то
ò f(x)dx = F(x) + C,
где С - произвольная постоянная.
Свойства неопределенного интеграла:
1) Производная от неопределенного интеграла равна подынтегральной функции, т.е.
(ò f(x)dx)′ = f(x)
2) Постоянный множитель можно выносить за знак интеграла, т.е.
ò a∙f(x)dx=a∙ò f(x)dx (a=const)
3) Интеграл от суммы (или разности) двух функций равен сумме (или разности) интегралов от этих функций, т.е.
ò (f(x) ±g(x))dx = ò f(x)dx ± ò g(x)dx.
Таблица основных интегралов
1. 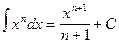 , (n ≠ -1)
, (n ≠ -1)
2. 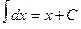
3. 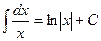
4. 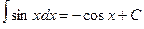
5. 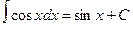
6. 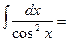 tg x + C
tg x + C
7. 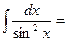 -ctg x+ C
-ctg x+ C
8. ∫ tg x dx = - 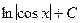
9. ∫ ctg x dx = 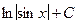
10. 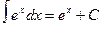
11. 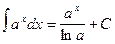
12. 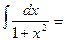 arctg x +C
arctg x +C
13. 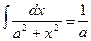 arctg
arctg 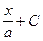
14. 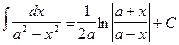
15. 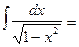 arcsin x + C
arcsin x + C
16. 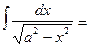 arcsin
arcsin 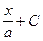
17. 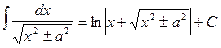
18. 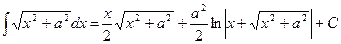
19. 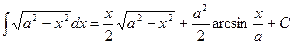
Дата добавления: 2020-06-09; просмотров: 592;











