Интегрирование рациональных дробей.
Для того чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
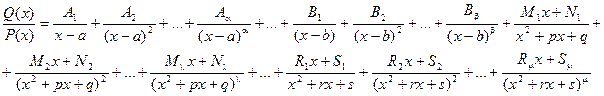
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Пример. 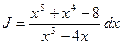 .
.
Подынтегральная дробь — неправильная, поэтому выделим её целую часть:
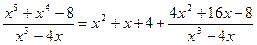 ;
;
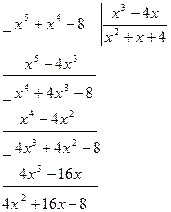
Проинтегрируем: 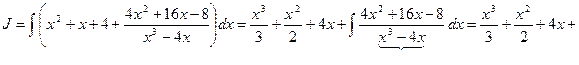
разложим на линейные множители
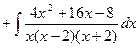
Правильную дробь 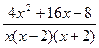 разложим на простейшие дроби и найдём коэффициенты A, B, C.
разложим на простейшие дроби и найдём коэффициенты A, B, C.
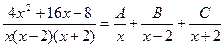 приведя правую часть равенства к общему знаменателю и отбросив последний, имеем:
приведя правую часть равенства к общему знаменателю и отбросив последний, имеем:
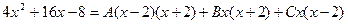
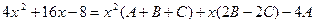
Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений для нахождения коэффициентов A, B, C.
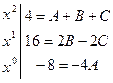
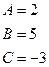
Таким образом, 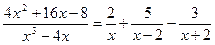
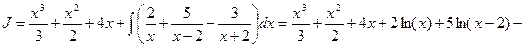
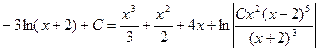
Пример. 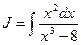
Правильную дробь 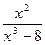 разложим на простейшие дроби.
разложим на простейшие дроби.
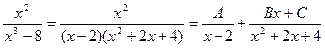
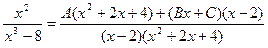
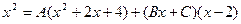
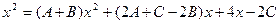

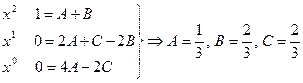
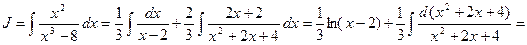
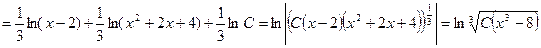
Пример. 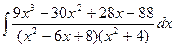
Т.к. ( 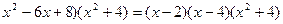 , то
, то
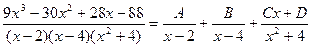
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
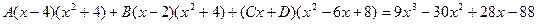
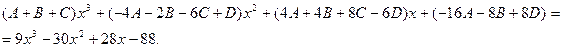
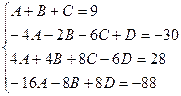
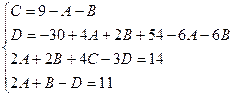
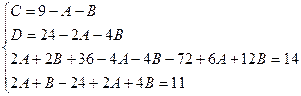
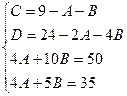
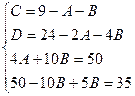
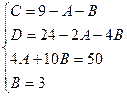
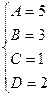
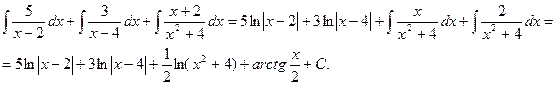
Пример. 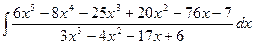
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
 6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
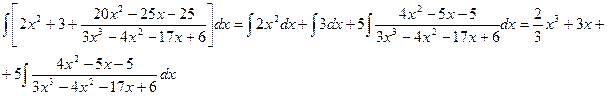
 Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
3x3 – 4x2 – 17x + 6 x - 3
3x3 – 9x2 3x2 + 5x - 2
5x2 – 17x
5x2 – 15x
- 2x + 6
-2x + 6
Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1).
Тогда 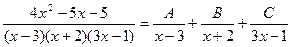
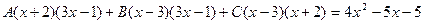
Для того чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
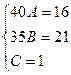
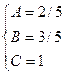
Окончательно получаем:
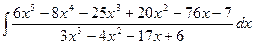 =
= 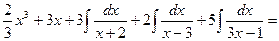
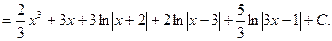
Пример. 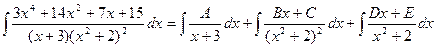
Найдем неопределенные коэффициенты:
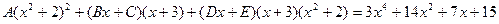
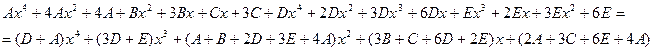
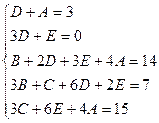
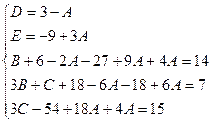
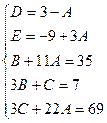
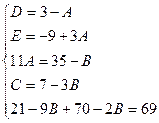
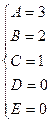
Тогда значение заданного интеграла:
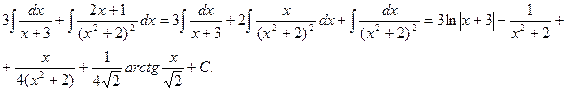
Дата добавления: 2020-06-09; просмотров: 567;











