Предел функции в точке

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена).

Число b называется пределом функции f(x) при х®а, если для любого e>0 существует такое число d(e) >0, что для всех х, удовлетворяющих неравенствам ïx - aï < d и x ≠ a верно неравенство

ïf(x) - bï< e.

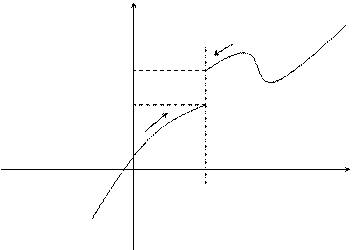
Геометрически определение предела означает, что если а - d < x < a + d, x ¹ a, то верно неравенство b - e < f(x) < b + e.

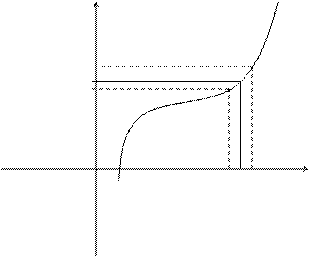y f(x)

A + e

A

A - e

0 a - D a a + D x

Запись предела функции в точке: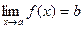

Если f(x) ® b при х ® а только при x < a, то 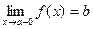- называется левым пределом функции f(x) в точке х = а, а если f(x) ® b при х ® а только при x > a, то 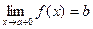называется правым пределом функции f(x) в точке х = а.

у

f(x)

b₂

b₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы b₁ и b₂ называются также односторонними пределами функции f(x) в точке х = а.

Предел функции при стремлении аргумента к бесконечности

Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

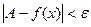
При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: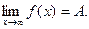

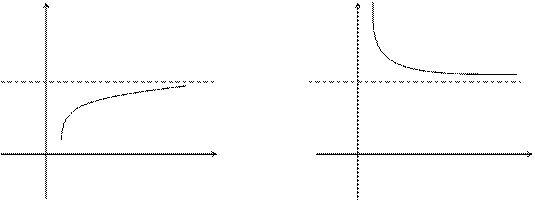
Графически можно представить:

y y

A A

0 0

x x

y y

A A

0 х 0 х

Аналогично можно определить пределы 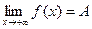для любого х>M и 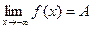для любого х<M.