РАЗДЕЛ 3. КОМПЛЕКСНЫЕ ЧИСЛА

Тема 3.1. Алгебраическая и геометрическая формы комплексного числа

Комплексным числомzназывается выражение вида 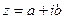, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частьючисла z (a = Re z), а b- мнимой частью (b = Im z).

Такая форма записи называется алгебраической формой комплексного числа.

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

Число 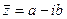называется сопряженным числу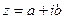

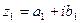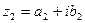Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части, т.е.

Действия с комплексными числами в алгебраической форме

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание:

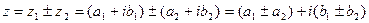
2) Умножение:

=

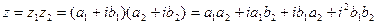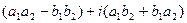
3) Деление:

=

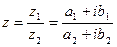
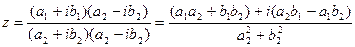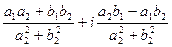
Пример. Даны два комплексных числа 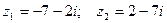. Найти значение выражения 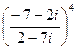в алгебраической форме.

Произведем деление двух комплексных чисел:

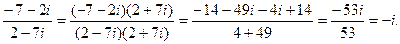
Получаем значение заданного выражения: 16(-i)⁴ = 16i⁴ =16.