Типы неопределенностей и методы их раскрытия
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.
I. Неопределенность вида 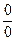 .
.
Пример. Вычислить предел 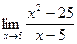
При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида 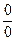 . Для ее раскрытия нужно разложить числитель на множители: (х2–25 = (х–5)∙(х+5)), получили общий множитель (х–5), на который можно сократить дробь. Заданный предел примет вид:
. Для ее раскрытия нужно разложить числитель на множители: (х2–25 = (х–5)∙(х+5)), получили общий множитель (х–5), на который можно сократить дробь. Заданный предел примет вид:  . Подставив х=5, получим результат.
. Подставив х=5, получим результат.
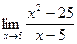 =
= 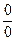 =
= 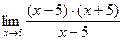 =
=  =5+5 =10
=5+5 =10
Пример. Вычислить предел 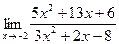
При подстановке вместо переменной х числа -2 видим, что получается неопределенность вида 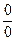 . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х+2. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа -2 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х+2. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа -2 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
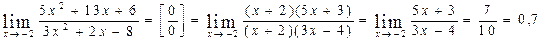
II. Неопределенность вида 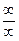 .
.
Для раскрытия этой неопределенности нужно каждое слагаемое числителя и знаменателя разделить на переменную в наибольшей степени и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность.
Пример. Вычислить предел 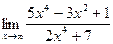
Здесь числитель и знаменатель не имеют предела, т.к. оба неограниченно возрастают. В этом случае имеем неопределенность вида 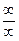 . Для ее раскрытия разделим каждое слагаемое на переменную в наибольшей степени, т.е. на х4. Получим:
. Для ее раскрытия разделим каждое слагаемое на переменную в наибольшей степени, т.е. на х4. Получим:
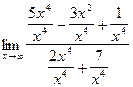 =
= 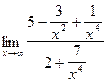 =
= 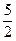
Величины 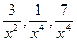 являются бесконечно малыми при
являются бесконечно малыми при 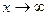 и их пределы равны нулю. Следовательно, искомый предел равен
и их пределы равны нулю. Следовательно, искомый предел равен 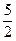 .
.
Пример. Вычислить предел 
Имеем неопределенность вида 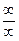 . Аналогично предыдущему примеру разделим числитель и знаменатель на х5. Получим:
. Аналогично предыдущему примеру разделим числитель и знаменатель на х5. Получим:
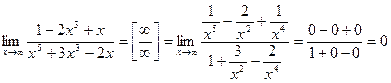
Пример. Вычислить предел 
Имеем неопределенность вида 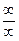 . Разделим числитель и знаменатель на х2. Получим:
. Разделим числитель и знаменатель на х2. Получим:
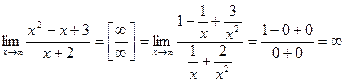
Дата добавления: 2020-06-09; просмотров: 723;











