Свойства функций, непрерывных на отрезке

Свойство 1: Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на этом отрезке наибольшее и наименьшее значения. Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m, f(x₂) = M, причем m £ f(x) £ M.

Свойство 3: Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

Свойство 4: Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает значения разных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Свойство 5: Если функция f(x) определена, монотонна и непрерывна на некотором отрезке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна на этом отрезке.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

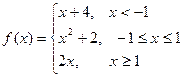
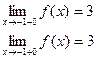
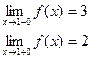
в точке х = -1 функция непрерывна х = 1 – точка разрыва 1–го рода

у

-4 -1 0 1 х

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

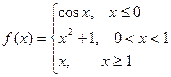
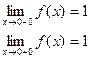
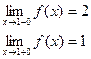
в точке х = 0 функция непрерывна х = 1 – точка разрыва 1–го рода

у

-p -p/2 0 1 x