Монотонные последовательности
1) Если xn+1 > xn для всех n, то последовательность возрастающая.
2) Если xn+1 ³ xn для всех n, то последовательность неубывающая.
3) Если xn+1 < xn для всех n, то последовательность убывающая.
4) Если xn+1 £ xn для всех n, то последовательность невозрастающая.
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример. {xn} = 1/n – убывающая и ограниченная
{xn} = n – возрастающая и неограниченная.
Пример. Доказать, что последовательность {xn}= 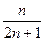 монотонная возрастающая.
монотонная возрастающая.
Найдем член последовательности {xn+1}= 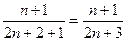
Найдем знак разности: {xn}-{xn+1}= 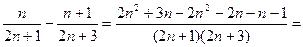
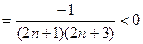 , т.к. nÎN, то знаменатель положительный при любом n.
, т.к. nÎN, то знаменатель положительный при любом n.
Таким образом, xn+1 > xn. Последовательность возрастающая, что и следовало доказать.
Пример. Выяснить является возрастающей или убывающей последовательность {xn}= 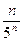 .
.
Найдем 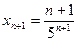 . Найдем разность
. Найдем разность 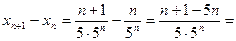
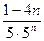 , т.к. nÎN, то 1 – 4n <0, т.е. хn+1 < xn. Последовательность монотонно убывает.
, т.к. nÎN, то 1 – 4n <0, т.е. хn+1 < xn. Последовательность монотонно убывает.
Теорема. Монотонная ограниченная последовательность имеет предел.
Число е
Рассмотрим последовательность {xn} = 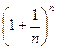 .
.
Эта последовательность 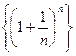 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
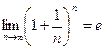
Можно показать, что число е иррациональное и его значение равно 2,71828…
Дата добавления: 2020-06-09; просмотров: 588;











