Классификация точек разрыва

1. Устранимый разрыв. Точка х₀ называется точкой устранимого разрыва функции, если в этой точке функция f(x) не определена, но имеет конечный предел.

2. Разрыв 1-го рода. Точка х₀ называется точкой разрыва 1-го рода функции, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.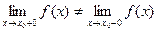

3. Разрыв 2-го рода. Точка х₀ называется точкой разрыва 2-го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция f(x) = 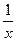имеет в точке х₀ = 0 разрыв 2–го рода, т.к.

.

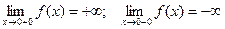Пример. f(x) =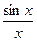

Функция не определена в точке х = 0, но имеет в ней конечный предел 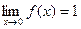, т.е. в точке х=0 функция имеет точку устранимого разрыва. Этот разрыв можно устранить, если доопределить функцию:

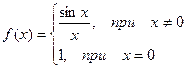
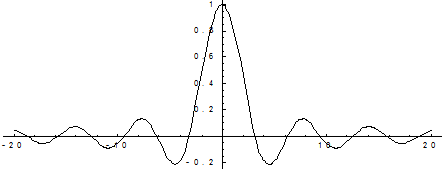
График этой функции:

Пример. f(x) = =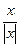

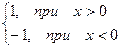
y

0 x

-1

Эта функция также обозначается sign(x). В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1–го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях будет иметь в точке х = 0 разрыв 1–го рода.