Миноры и алгебраические дополнения элементов определителя
Пусть дана матрица 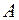
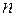 -го порядка.
-го порядка.
Минором любого элемента 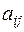 называют определитель порядка
называют определитель порядка 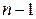 , соответствующий той матрице, которая получается из матрицы
, соответствующий той матрице, которая получается из матрицы 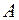 в результате вычеркивания
в результате вычеркивания 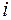 -й строки и
-й строки и 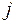 -го столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент
-го столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент 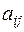 ). Минор элемента
). Минор элемента 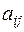 будем обозначать символом
будем обозначать символом 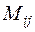 .
.
Алгебраическим дополнением 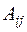 элемента
элемента 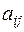 матрицы
матрицы 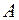 называют минор
называют минор 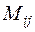 этого элемента, умноженный на
этого элемента, умноженный на 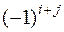 , т.е.
, т.е.
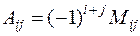 .
.
Вычисление определителей п-го порядка
Теорема. Определитель матрицы 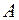
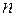 -го порядка равен сумме произведений всех элементов какой-нибудь одной фиксированной строки на их алгебраические дополнения, т.е. для любого
-го порядка равен сумме произведений всех элементов какой-нибудь одной фиксированной строки на их алгебраические дополнения, т.е. для любого 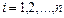 имеет место равенство
имеет место равенство
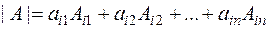 ,
,
называемое разложением определителя 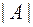 по элементам
по элементам 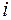 -й строки.
-й строки.
Аналогично для 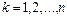 имеет место разложение определителя
имеет место разложение определителя 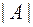 по элементам k-го столбца:
по элементам k-го столбца:
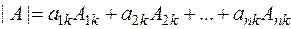 .
.
Способы вычисления определителей:
- Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно вычислять определители второго и третьего порядка.
- Определитель можно вычислить с помощью его разложения по элементам строки или столбца.
- Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 9треугольный определитель равен произведению элементов главной диагонали.
Чтобы получить треугольный определитель, нужно к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор, пока не придем к определителю треугольного вида.
Пример. Вычислить определитель матрицы А = 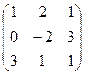

= -5 + 18 + 6 = 19.
Пример: Даны матрицы А = 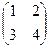 , В =
, В = 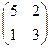 . Найти det (AB).
. Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.
2- й способ: AB = 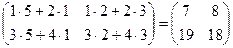 , det (AB) = 7×18 - 8×19 = 126 – 152 = -26.
, det (AB) = 7×18 - 8×19 = 126 – 152 = -26.
Пример. Вычислить определитель 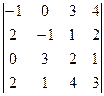 .
.
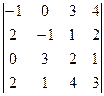 = -1
= -1 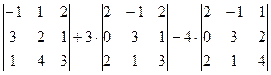
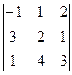 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
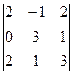 =
= 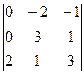 = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2.
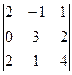 =
= 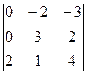 = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.
Значение определителя: -10 + 6 – 40 = -44.
Упражнение. Вычислите каждый из следующих определителей двумя способами (с помощью правила треугольников и с помощью разложения по элементам строки или столбца):
а) 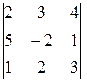 , б)
, б) 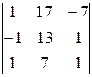 , в)
, в) 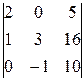 .
.
Обратная матрица
Квадратная матрица 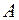 называется невырожденной, если ее определитель отличен от нуля (
называется невырожденной, если ее определитель отличен от нуля ( 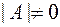 ). В противном случае матрица
). В противном случае матрица 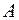 называется вырожденной(
называется вырожденной( 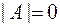 ).
).
Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая при умножении на матрицу А (как слева, так и справа) дает единичную матрицу. Обратная матрица обозначается символом 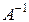 .
.
Если для квадратной матрицы 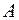 существует обратная матрица
существует обратная матрица 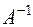 , то справедливо равенство
, то справедливо равенство 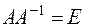 , где
, где 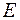 – единичная матрица.
– единичная матрица.
Пусть матрица 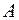 имеет вид:
имеет вид:
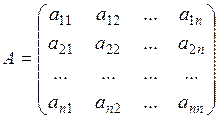 .
.
Теорема. Если 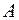 – невырожденная матрица, то для нее существует обратная матрица
– невырожденная матрица, то для нее существует обратная матрица 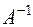 , которая вычисляется по формуле
, которая вычисляется по формуле
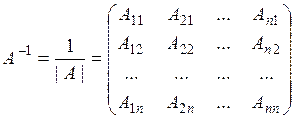 ,
,
где 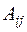 – алгебраическое дополнение для элемента
– алгебраическое дополнение для элемента 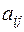 матрицы
матрицы 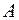 .
.
Дата добавления: 2020-06-09; просмотров: 813;











