Свойства обратных матриц
1) (A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T.
Пример. Дана матрица А = 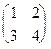 , найти А-1.
, найти А-1.
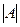 = 4 – 6 = – 2
= 4 – 6 = – 2
А11 = 4; А12 = – 3; А21 = – 2; А22 = 1
Таким образом, 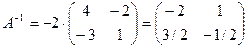 .
.
Упражнение. Найти обратные для следующих матриц и проверить результат:
а) 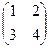 , б)
, б) 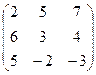 , в)
, в) 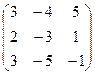 .
.
Ранг матрицы
Ранее для квадратной матрицы 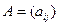
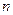 -го порядка было введено понятие минора
-го порядка было введено понятие минора 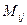 элемента
элемента 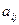 . Так был назван определитель порядка
. Так был назван определитель порядка 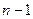 , полученный из определителя
, полученный из определителя 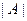 вычеркиванием
вычеркиванием 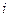 -й строки и
-й строки и 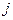 -го столбца.
-го столбца.
Введем теперь общее понятие минора. Рассмотрим некоторую, не обязательно квадратную матрицу 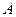 . Выберем какие-нибудь
. Выберем какие-нибудь 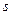 номеров строк
номеров строк 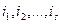 и
и 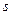 номеров столбцов
номеров столбцов 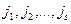 .
.
Минором порядка 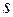 матрицы
матрицы 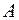 (соответствующим выбранным строкам и столбцам) называется определитель порядка
(соответствующим выбранным строкам и столбцам) называется определитель порядка 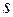 , образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число
, образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число
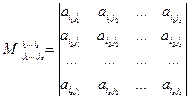 .
.
Каждая матрица имеет столько миноров данного порядка 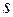 , сколькими способами можно выбрать номера строк
, сколькими способами можно выбрать номера строк 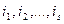 и столбцов
и столбцов 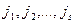 .
.
В матрице 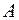 размеров
размеров 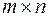 минор порядка
минор порядка 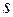 называется базисным, если он отличен от нуля, а все миноры порядка
называется базисным, если он отличен от нуля, а все миноры порядка 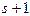 равны нулю или миноров порядка
равны нулю или миноров порядка 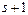 вообще нет, т.е.
вообще нет, т.е. 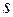 совпадает с меньшим из чисел m или n.
совпадает с меньшим из чисел m или n.
Ясно, что в матрице может быть несколько разных базисных миноров. Все базисные миноры имеют один и тот же порядок.
Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.
Ранг матрицы 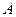 обозначается символом
обозначается символом 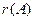 или RgA. Из определения ранга следует, что для матрицы
или RgA. Из определения ранга следует, что для матрицы 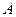 размеров
размеров 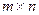 справедливо соотношение
справедливо соотношение 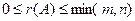 .
.
Дата добавления: 2020-06-09; просмотров: 745;











