Метод Крамера для решения систем линейных уравнений

Пусть дана система 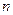линейных уравнений с 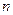неизвестными:

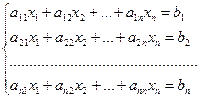
Составим матрицы: А = 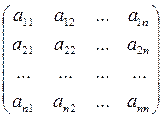и В =

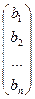
Определитель 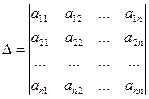, составленный из коэффициентов при неизвестных, называется определителем системы.

Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Это решение может быть найдено по формулам

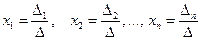, где

, , …,

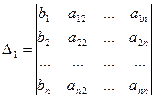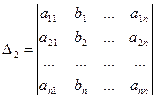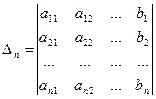
Пример. Решить систему уравнений методом Крамера: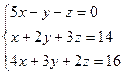

D = 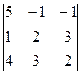= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D₁ = 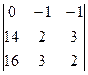= (28 – 48) – (42 – 32) = -20 – 10 = -30.

D₂ = 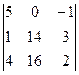= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

D₃ = 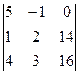= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x₁ = 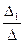= 1; x₂ = 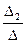= 2; x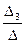₃ = = 3.

Для самостоятельного решения:

;

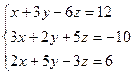Решение произвольных систем линейных уравнений

Как было сказано выше, матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений.

Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

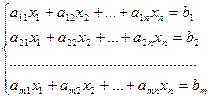где a_ij – коэффициенты, а b_i – постоянные. Решением системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Для этой системы линейных уравнений вида матрица

А = 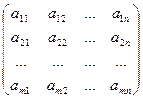называется матрицей системы, а матрица

А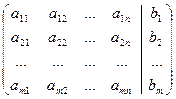^*= называется расширенной матрицей системы