Идея практического метода вычисления ранга матрицы
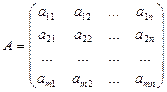
заключается в том, что с помощью элементарных преобразований данную матрицу 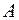 приводят к виду
приводят к виду
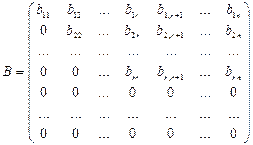 ,
,
в котором «диагональные» элементы 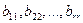 отличны от нуля, а элементы, расположенные ниже «диагональных», равны нулю. Матрица
отличны от нуля, а элементы, расположенные ниже «диагональных», равны нулю. Матрица 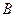 такого вида называется треугольной (или трапециевидной). После приведения матрицы
такого вида называется треугольной (или трапециевидной). После приведения матрицы 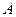 к треугольному виду можно сразу записать, что
к треугольному виду можно сразу записать, что 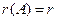 .
.
В самом деле, 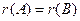 (т.к. элементарные преобразования не меняют ранга). Но у матрицы
(т.к. элементарные преобразования не меняют ранга). Но у матрицы 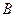 существует отличный от нуля минор порядка
существует отличный от нуля минор порядка 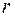 :
:
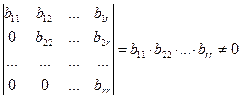 ,
,
а любой минор порядка 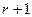 содержит нулевую строку и поэтому равен нулю.
содержит нулевую строку и поэтому равен нулю.
Сформулируем теперь практическое правило вычисления ранга матрицы 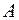 с помощью элементарных преобразований: для нахождения ранга матрицы
с помощью элементарных преобразований: для нахождения ранга матрицы 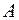 следует с помощью элементарных преобразований привести ее к треугольному виду
следует с помощью элементарных преобразований привести ее к треугольному виду 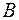 . Тогда ранг матрицы
. Тогда ранг матрицы 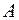 будет равен числу ненулевых строк в полученной матрице
будет равен числу ненулевых строк в полученной матрице 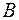 .
.
Пример. Определить ранг матрицы.
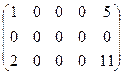 ~
~ 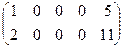 ~
~ 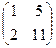 ,
, 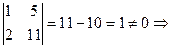 RgA = 2.
RgA = 2.
Пример: Определить ранг матрицы.
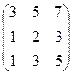 ~
~ 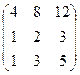 ~
~ 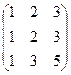 ~
~ 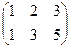 ,
, 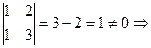 Rg = 2.
Rg = 2.
Пример. Определить ранг матрицы.
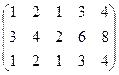 ~
~ 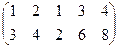 ,
, 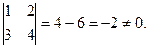 Þ Rg = 2.
Þ Rg = 2.
Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.
Упражнение. Найти методом элементарных преобразований ранг матрицы
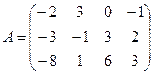 .
.
Дата добавления: 2020-06-09; просмотров: 760;











