Элементарные преобразования систем
1) Умножение или деление коэффициентов и свободных членов на одно и то же число
2) Сложение и вычитание уравнений
3) Перестановка уравнений системы местами.
4) Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в том, что систему уравнений приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называются прямым ходом. Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
Пример. Решить систему линейных уравнений методом Гаусса 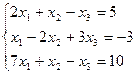
Составим расширенную матрицу системы.
А* = 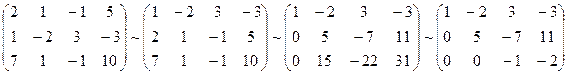
Таким образом, исходная система может быть представлена в виде:
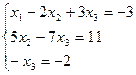 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Пример. Решить систему линейных уравнений методом Гаусса 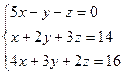
Составим расширенную матрицу системы.
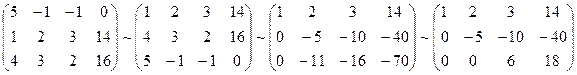
Таким образом, исходная система может быть представлена в виде:
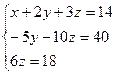 , откуда получаем: z = 3; y = 2; x = 1.
, откуда получаем: z = 3; y = 2; x = 1.
Для самостоятельного решения:
1) 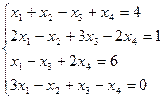
2) 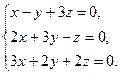
Дата добавления: 2020-06-09; просмотров: 701;











