Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

А×Е = Е×А = А

Перестановочными могут быть только квадратные матрицы одного и того же порядка. Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O, где О – нулеваяматрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ, то определено произведение В^ТА^Т и выполняется равенство:

(АВ)^Т = В^ТА^Т

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB. Что такое det будет рассмотрено ниже.

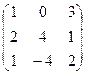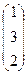Пример. Даны матрицы А = , В = , С = 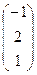и число a = 2.

Найти А^ТВ+aС.

A^T = 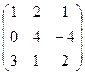; A^TB = 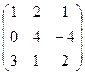× 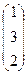= = 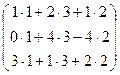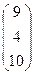; aC = 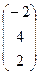; А^ТВ+aС = + = .

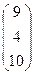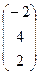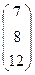Пример. Найти произведение матриц А = 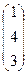и В = .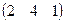

АВ = × = .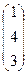

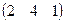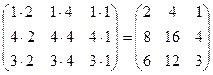ВА = 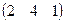× 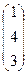= 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

Пример. Найти произведение матриц А= 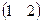, В =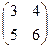

АВ = × = = .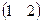

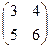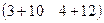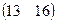Определители

Каждой квадратной матрице 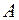может быть поставлено в соответствие некоторое число, вычисляемое по определенному правилу с помощью элементов матрицы. Такое число называют определителем(или детерминантом) матрицы 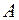и обозначают символом 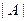или 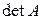. При этом порядком определителя называют порядок соответствующей матрицы.

Определитель 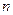-го порядка имеет вид: .

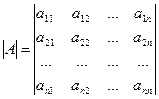Правила вычисления определителей 2-го и 3-го порядков легко выписать:

,

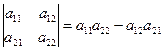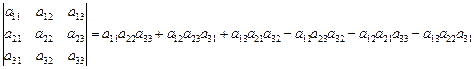
Последнюю формулу, несмотря на внешнюю сложность записи, нетрудно запомнить. Если соединить линией каждые три элемента определителя, произведение которых входит в правую часть последней формулы со знаком « 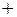», то получим легко запоминающуюся схему 1. Аналогично для произведений, входящих со знаком «–», имеем схему 2.

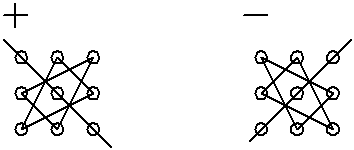Схема 1 Схема 2

Это правило вычисления определителей 3-го порядка называется правилом треугольников (или правилом Сарруса).