Дифференциальное уравнение теплопроводности

Математическое описание температурных полей в элементах технологических систем под действием внешнего источника теплоты выполняется с помощью дифференциального уравнения теплопроводности

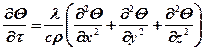, (1.22)

где с – объемная теплоемкость материала,

ρ – плотность материала.

Это уравнение справедливо при следующих допущениях:

- твердое тело однородно и изотропно;

- в процессе теплообмена не происходят фазовые превращения, т.е. отсутствуют внутренние источники теплоты.

Величина 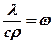называется коэффициентом температуропроводности. С увеличением ω возрастает скорость изменения температуры в данной точке. В материале с более высоким коэффициентом температуропроводности выравнивание температур будет проходить быстрее.

Часто уравнение (1.22.) записывают так:

,

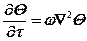где 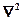– оператор Лапласа.

Выражение (1.22) представляет собой линейное дифференциальное уравнение в частных производных второго порядка.

Для установившегося теплообмена и стационарного температурного поля .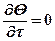

Тогда (1.23)

Это дифференциальное уравнение для трехмерного стационарного температурного поля.

Аналогично:

при 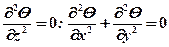– для двумерного поля, (1.24)

при 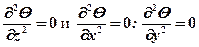– для одномерного поля. (1.25)

Вопросы для самопроверки

1. Равен ли коэффициент теплопроводности тела с внутренними пустотами коэффициенту теплопроводности материала из которого изготовлено это тело? Больше он или меньше? Как учесть влияние пустот?

2. Сопоставьте между собой тепловые сопротивления двух стержней квадратного сечения, изготовленных из одного и того же материала, если стержень 1 имеет в 2 раза большую длину и в 2 раза большую площадь поперечного сечения, чем стержень 2. Рассмотрите два варианта: – тепловой поток направлен через торец вдоль оси стержней; – тепловой поток направлен через боковую поверхность перпендикулярно оси стержней.

3. Напишите дифференциальные уравнения теплопроводности: – для двумерного поля при установившемся теплообмене; – для одномерного нестационарного поля.

Задачи

1. Рассчитать коэффициент теплопроводности углеродистой инструментальной стали У12 (С = 1,2 %; Мn = 0.2 %; Si = 0,3 %;

S = 0.02 %; Р = 0,03 %) при температуре 400 °С.

2. Рассчитать коэффициент теплопроводности хромоникелевой аусте-нитной стали 45XI4H14B2M при температуре 500 °С. Атомные массы С = 12; Сг = 52; Ni = 59; W= 184; Mo = 96

3. Рассчитать эквивалентный коэффициент теплопроводности алмазного круга на бакелитовой связке. Всего в объеме содержится: зерна алмаза синтетического – 25 % (λ=520 Вт/м°С), зерна карбида бора – 25 % (λ = 16 Вт/м°С), бакелитовая связка – 48 % (λ = 0,2 Вт/м°С), воздушные поры – 2 % (λ = 0,03 Вт/м°С).

4. На стальной заготовке прорезают паз резцом с пластинкой Т15К6

(λ = 27 Вт/м°С). Скорость резания составляет 40 м/мин, сила резания P_z = 2295 Н. Температура опорной поверхности державки резца Θ₂ = 60 °С. Материал державки – сталь 45 (λ = 40 Вт/м°С).

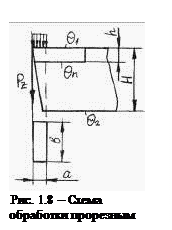В резец отводится 5 % образующейся теплоты, в сторону опорной поверхности отводится 12 % теплоты, отводящейся в резец. Размеры контактной площадки на передней поверхности а = 1,8 мм, b = 4 мм.

Определить среднюю температуру на передней поверхности резца Θ₁,определить среднюю температуру на стыке пластинки с державкой Θ_n. Определить температуру на передней поверхности Θ₁, если вместо твердосплавной будет установлена алмазная поликристаллическая пластина (λ = 520 Вт/м°С).

5. При запрессовке биметаллической втулки, состоящей из двух слоев – наружный сталь 40Х (λ = 33,9 Вт/м°С), внутренний – бронза (λ = 68 Вт/м°С), наружная поверхность нагревается до температуры Θ_Н = 800°C. Мощность, затрачиваемая на нагрев, W = 2,5 кВт Определить температуру внутренней поверхности Θ_в.

Размеры втулок: D = 40 мм, d₁ = 30 мм, d = 20 мм, l = 40 мм.