Коэффициенты теплопроводности тел
Коэффициенты теплопроводности твердых тел определяются экспериментально и зависят от их химического состава и температуры.
На рис.1.6 показаны зависимости l (q) для некоторых металлов
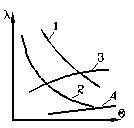
1 – твердый сплав
2 – углеродистая сталь
3 – быстрорежущая сталь
4 – жаропрочный титановый сплав
Рис. 1.6 – Зависимость коэффициентов теплопроводности от температуры
Из рисунка видно, что зависимости коэффициента теплопроводности от температуры имеют сложный вид. Значения коэффициентов теплопроводности приводятся в таблицах, либо рассчитываются по опытным формулам. Для углеродистых малолегированных сталей – конструкционных, инструментальных, формула для расчета коэффициентов теплопроводности имеет вид
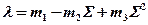 , (1.17)
, (1.17)
где S – суммарное содержание всех добавок к железу, включая углерод, в %;
m1, m2, m3 – опытные коэффициенты, зависящие от температуры. Эти коэффициенты определяются по формуле
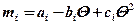 ,
,
где Θ – температура металла.
Значения коэффициентов ai bi ci приведены в таблице 1.1.
Таблица 1.1 – Коэффициенты для расчета l углеродистых сталей.
| Коэффициенты | ai | bi | ci |
| m1 | 76,8 | 6,67*10–2 | |
| m2 | 34,2 | 9,88*10–2 | 8,14*10–5 |
| m3 | 9,3 | 3,95*10–2 | 4,18*10–5 |
Для высоколегированных сталей расчет коэффициентов теплопроводности можно производить по формуле
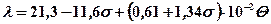 , (1.18)
, (1.18)
где величина s представляет собой сумму
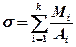 ,
,
Mi – процентное содержание добавки к железу, включая углерод,
Ai – атомная масса элемента, образующего легирующую добавку.
k – число легирующих добавок в составе стали.
В технологических системах встречаются тела, представляющие собой ту или иную композицию из материалов с различными физико-механическими свойствами.
Эти композиции могут состоять из элементов, расположенных регулярно, т.е. в заданном порядке – слоями (биметаллические втулки, покрытия), или элементов, расположенных стохастически, т.е. хаотично (шлифовальные круги). Для определения коэффициентов теплопроводности неоднородных тел используют эквивалентный коэффициент теплопроводности lЭ.
Рассмотрим плоскую стенку, состоящую из отдельных слоев толщиной D1, D2, D3 с коэффициентами теплопроводности l1, l2, l3 (рис.1.7)
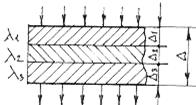
Рис.1.7 – Схема плоской стенки, состоящей из нескольких слоев.
Если тепловой поток проходит последовательно через все слои, то тепловое сопротивление всей стенки (по аналогии с электрическими цепями) равно сумме тепловых сопротивлений всех слоев.
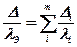 ,
,
откуда
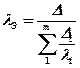 , (1.19)
, (1.19)
где m – число слоев.
Аналогичную формулу можно получить для расчета эквивалентного коэффициента теплопроводности многослойной втулки.
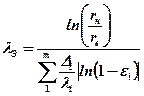 , (1.20)
, (1.20)
где rн и rв – радиусы наружной и внутренней поверхности втулки,
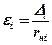 .– безразмерный коэффициент;
.– безразмерный коэффициент;
rнi – радиусы наружных поверхностей слоев втулки,
Δi – толщины слоев втулки,
λi – коэффициенты теплопроводности материалов слоев втулки,
m – число слоев.
В случае стохастического расположения частей для расчета эквивалентного коэффициента теплопроводности тела можно использовать формулу
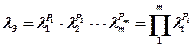 , (1.21)
, (1.21)
где λi – коэффициенты теплопроводности отдельных элементов;
Pi – относительная объемная концентрация элементов (в долях), т.е. ΣPi = 1;
m – число элементов.
Дата добавления: 2020-06-09; просмотров: 595;











