Схематизация по виду закона распределения плотности тепловыделения
Выделим в трехмерном источнике тепловыделения точку М с координатами 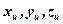 (индекс u – относится к источнику). Если процесс теплообмена установившийся, то элементарное количество теплоты dQ выделившейся за время τ в элементарном объеме dV будет равно
(индекс u – относится к источнику). Если процесс теплообмена установившийся, то элементарное количество теплоты dQ выделившейся за время τ в элементарном объеме dV будет равно
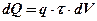 , (2.1)
, (2.1)
где q – плотность тепловыделения в точке М.
Величина 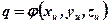 зависит для установившегося процесса от координат точки М и имеет сложный вид.
зависит для установившегося процесса от координат точки М и имеет сложный вид.
Для удобства вычислений величину q можно представить следующим образом
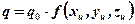 , (2.2)
, (2.2)
где q0 – максимальная плотность тепловыделения;
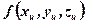 – функция, описывающая закон распределения тепловыделения в объеме и являющаяся безразмерной. Количество теплоты, выделившейся в объеме V за время τ определяем, интегрируя выражение (2.1.)
– функция, описывающая закон распределения тепловыделения в объеме и являющаяся безразмерной. Количество теплоты, выделившейся в объеме V за время τ определяем, интегрируя выражение (2.1.)
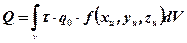
Учитывая, что 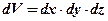 ,
,
имеем 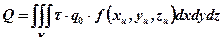
Величины τ и q0 являются постоянными.
Тогда
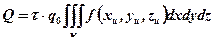
Обозначим интеграл 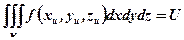
В этом случае
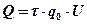 (2.3.)
(2.3.)
Функция U будет иметь вид:
- для трехмерного источника
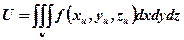
- для двумерного источника
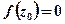
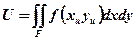
- для одномерного источника
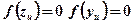 ,
,
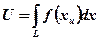
Из формулы (2.3.)
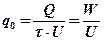 (2.4)
(2.4)
где W – средняя мощность тепловыделения.
Максимальная плотность тепловыделения q0 имеет размерность:
- для трехмерного источника Вт/м3
- для двумерного источника Вт/м2
- для одномерного источника Вт/м
- для точечного источника Вт
Для действующих реальных источников теплоты вид зависимости 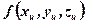 достаточно сложен. Поэтому эту безразмерную функцию заменяют некоторой схематизированной.
достаточно сложен. Поэтому эту безразмерную функцию заменяют некоторой схематизированной.
Закон распределения плотности тепловыделения может быть установлен только вдоль одной оси, т.е. только для одномерного источника 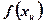 .
.
Двумерные и трехмерные источники представляют собой комбинации законов распределения по двум или трем осям.
Схематизированные законы распределения плотности тепловыделения источников приведены в таблице (2.2)
Таблица 2.2 – Законы распределения плотности тепловыделения.
| код | График закона распределения | Закон | Функция f(xu) |
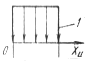
| Равномерно распределенный | f(xu) = 1 | |
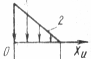
| Линейный | f(xu) = 1 – ψu |
Продолжение таблицы 2.2
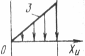
| Линейный | f(xu) = ψu | |

| Экспоненциальный | f(xu) = exp[ - k0xu] | |

| Нормально распределенный несимметричный | 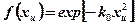
| |

| Нормально распределенный несимметричный | f(xu) = exp[ – k0(l – xu)2] | |
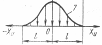
| Нормально распределенный симметричный | 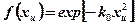
| |
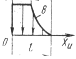
| Комбинированный | f(xu) = 1 f(xu) = exp[ – k0(ψu – 0,5)] |
В этой таблице величины ψu и k0 – параметры распределения.
Код закона распределения плотности тепловыделения источника или стока теплоты содержит 3 цифры, т.е. определяет законы распределения по каждой из осей, что соответствует трехмерному источнику.
Для двумерных источников одна из цифр в коде будет нулем, т.к. по одной из осей распределения нет.
Если источник одномерный, то код содержит два нуля, т.к. распределение плотности тепловыделения будет только по одной оси.
Для точечного источника код содержит три нуля.
При решении теплофизических задач обычно известно количество выделившейся теплоты Q за время действия источника τ, т.е. известна тепловая мощность источника W. Требуется определить q0 – максимальную плотность тепловыделения для разных значений функции U, т.е. разных законов распределения.
В большинстве случаев при рассмотрении процессов теплообмена в элементах технологических систем, связанных с операциями механической обработки и металлорежущими станками, источники и стоки теплоты являются двумерными, т.е. представляют собой плоские фигуры. Рассмотрим некоторые примеры двумерных источников. В этом случае функция
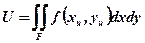
Код распределения 101 – двумерный источник, равномерно распределенный вдоль двух осей (рис.2.3.)
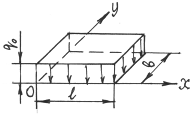
Рис. 2.3 – Источник с кодом 101
По таблице (2.2.)
f(x) = 1, f(y) = 1
x изменяется от 0 до l,
y изменяется от 0 до b
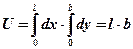 ,
,
откуда 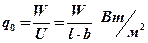 (2.5)
(2.5)
Код распределения 201 – двумерный источник распределен по линейному закону вдоль оси x и равномерно вдоль оси y (рис.2.4)
По таблице (2.2)
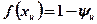 , где
, где 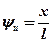 ,
, 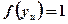
x изменяется от 0 до l,
y изменяется от 0 до b
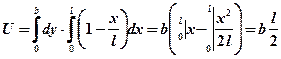 ;
;
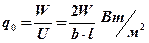 (2.6)
(2.6)
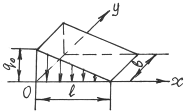
Рис. 2.4 – Источник с кодом 201
Код распределения 501 – двумерный источник распределен по нормальному несимметричному закону по оси x и равномерно по оси y (рис.2.5)
По таблице
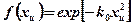
x изменяется от 0 до l,
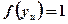
y изменяется от 0 до b
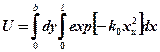 ,Интеграл
,Интеграл 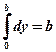
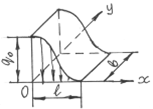
Рис. 2.5 – Источник с кодом 501
Интеграл 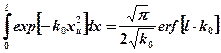 ,
,
где 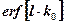 – интеграл вероятности, значения которого табулированы (называется «эрфект»). Таким образом
– интеграл вероятности, значения которого табулированы (называется «эрфект»). Таким образом
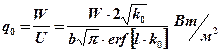 . (2.7)
. (2.7)
Код распределения 801 – двумерный источник распределен по комбинированному закону по оси x и равномерно по оси y (рис.2.6)
После интегрирования получаем
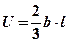
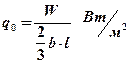 (2.8)
(2.8)
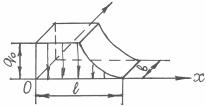
Рис. 2.6 – Источник с кодом 801
Код распределения 101 – двумерный круговой источник с равномерным распределением (рис.2.7)
После интегрирования получаем
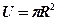 , где R – радиус источника
, где R – радиус источника
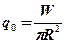 (2.9)
(2.9)
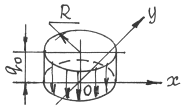
Рис. 2.7 – Круговой источник с кодом 101
Код распределения 707 – двумерный круговой источник с нормальным законом распределения (рис.2.8)
После интегрирования получаем
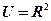 , где R – радиус пятна нагрева
, где R – радиус пятна нагрева
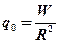 (2.10)
(2.10)
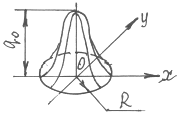
Рис. 2.8 – Источник с кодом 707
Аналогично рассчитывают величину q0 для источников с другими законами распределения.
Дата добавления: 2020-06-09; просмотров: 744;











