Оптимизация периода длительных профилактических ремонтов

Одним из методов повышения технологической надежности является профилактический ремонт машин и механизмов. Циклический характер позволяет приурочить его полностью или частично к периодам технологических перерывов в работе механизма.

Профилактический ремонт позволяет уменьшить количество и длительность аварийных ремонтов, а следовательно, и простои оборудования. Однако длительный профилактический ремонт сам ведет к простою механизма и снижению его производительности. Существующие нормативные документы по проведению профилактических ремонтов не учитывают ни надежности машин, ни принятой технологической схемы.

На рис. 6.8, а приведена схема комплекса оборудования, состоящего из ведущего механизма А и вспомогательного механизма Б, работающих в такой последовательности. Во время аварийного ремонта механизма А механизм Б простаивает; по окончании ремонта начинает действовать механизм Б, который работает неполный период и выполняет объем работ, подготовленный механизмом А до его ремонта. После завершения работы механизмом Б начинает снова работать механизм А.

Коэффициент простоя на промежутке (0,t) выражается по формуле

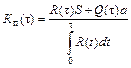_, (6.12)

где Q(t) - функция распределения случайного времени исправной работы механизма А на данном промежутке; R(t) - функция надежности; a - длительность аварийного ремонта; 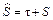- длительность профилактического ремонта.

Здесь t - время технологического перерыва механизма А (или рабочий период механизма Б).

Время t принимается кратным r - рабочему периоду механизма А t = mr (m = 0, 1, 2,…).

Из формулы (6.12) определяется число полных рабочих периодов m*, после которых необходим профилактический ремонт, чтобы коэффициент простоя был минимальным, m* = [t*/r], где t* находится как корень уравнения

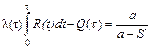_, (6.13)

где 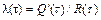- опасность отказа.

Функция Q(t) определяется из опыта путем наблюдений за работой машины (рис. 6.8). Обычно опасность отказов l(t) является неубывающей функцией, исключая лишь начальный период эксплуатации машины (период приработки, когда обнаруживаются скрытые дефекты изготовления). Поэтому в качестве Q(t) принимается закон Вейбулла

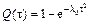_, (6.14)

для которого l₀ = p/2×1/2T_ср²,

Т_ср - среднее время безотказной работы машины.

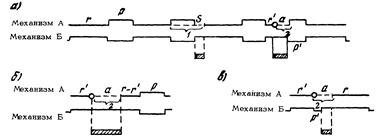
Рис. 6.8. Схема расчета коэффициента простоя системы машин и механизмов для различных технологических схем:

1 - профилактический ремонт; 2 - аварийный; время ремонта; - момент отказа механизма; остальные обозначения см. на рис. 6.6

Для схемы, представленной на рис. 6.8, б, возможна ситуация, когда во время аварийного ремонта механизма А механизм Б также простаивает. Но после окончания ремонта сначала вновь включается механизм А, который должен работать столько времени, чтобы его суммарное время работы до аварийного ремонта r¢ и после него 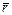было равно полному рабочему периоду r, и только после этого включается механизм Б. В этом случае формулы (6.9) и (6.10) остаются верными, если в них заменить t на 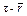, а следовательно, t* заменить на .

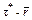Если во время аварийного ремонта механизма А механизм Б работает и выполняет объем работ, подготовленный ведущим механизмом до аварийного ремонта (см. рис. 6.8., в), то потери времени при эксплуатации комплекса равны a - qr¢ при a > qr¢.

Тогда коэффициент простоя

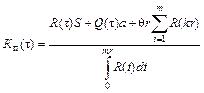
(6.15)

Следует отметить, что K_п(mr) - функция, имеющая несколько минимумов; однако, задав степень точности e, можно найти требуемый минимум.

Если горно-проходческий комплекс состоит из l механизмов, подверженных отказам в период их работы, то коэффициент простоя комплекса K_п^комп выразится через коэффициенты простоя отдельных механизмов K_пⁱ:

1) в случае последовательной работы механизмов

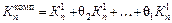(6.16)

где q_i = r_i/p_i (r_i - время работы i-го механизма на цикле; p_i - время технологического перерыва i-го механизма на цикле);

2) в случае одновременной работы механизмов

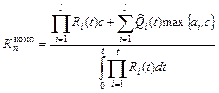, (6.17)

где 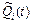- вероятность того, что комплекс имел отказ на (0, t) вследствие аварии механизма A_i; a_i - продолжительность аварийного ремонта механизма A_i;

Оптимизация коэффициента простоя в случае последовательной работы комплекса производится по каждому механизму в отдельности. При одновременной работе нескольких механизмов формула (6.13) даст для этого варианта оценку сверху.

В случае распределения Вейбулла 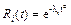(a > 1),положив для простоты mina_i ³ c, можно получить

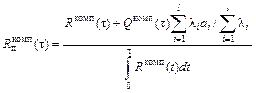_, (6.18)

где _.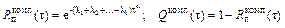

В общем случае вероятности 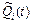можно определять также из статистических материалов, например, сопоставляя гистограммы распределения Q_i(t).